题目内容
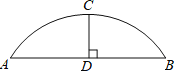
【题目】我国古代数学著作《九章算术》中记载了弓形面积的计算方法.如图,弓形的弦长AB为30![]() cm,拱高(弧的中点到弦的中点之间的距离)CD为15cm,则这个弓形的面积是( )cm2.
cm,拱高(弧的中点到弦的中点之间的距离)CD为15cm,则这个弓形的面积是( )cm2.
A.300π-450![]() B.900π-225
B.900π-225![]() C.900π-450
C.900π-450![]() D.300π-225
D.300π-225![]()
【答案】D
【解析】
设弧ACB所在圆的圆心为O,连接OC、OA、OB,在构造的Rt△OAD中,利用垂径定理和勾股定理即可求出弧ACB的半径长,即弓形面积=扇形AOB面积-△AOB面积.
解:设弧ACB所在圆的圆心为O,连接OC、OA、OB,
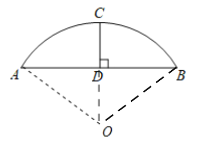
∵CD⊥AB,
∴C,D,O三点共线,
在Rt△OAD中,设OA=xcm,则OD=x-CD=(x-15)cm,![]() (cm),
(cm),
∴![]() ,
,
即![]() ,
,
解得:![]() 0,
0,
∴OD=15cm,AO=30,
∴∠OAD=30°,
∴∠AOD=60°,
∴∠AOB=120°,
∴![]() ,
,![]() ,
,
所以所求弓形面积![]() ,
,
故选:D.

练习册系列答案
相关题目