题目内容
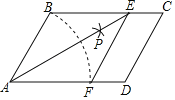
【题目】如图,在ABCD中,AB=3,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于![]() BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则四边形ABEF的周长为( )
BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则四边形ABEF的周长为( )
A.12B.14C.16D.18
【答案】A
【解析】
利用基本作图得到AB=AF=3,∠BAE=∠FAE,根据平行四边形的性质得BC∥AD,则∠BEA=∠FAE,所以∠BAE=∠BEA,从而得到BE=BA=3,于是可判断四边形ABEF为菱形,于是得到四边形ABEF的周长.
由作法得AB=AF=3,AE平分∠BAD,
∴∠BAE=∠FAE,
∵四边形ABCD为平行四边形,
∴BC∥AD,
∴BE∥AF
∴∠BEA=∠FAE,
∴∠BAE=∠BEA,
∴BE=BA=3,
∴BE=AF
∴四边形ABEF为平行四边形,
∵AB=AF
∴四边形ABEF为菱形,
∴四边形ABEF的周长=4×3=12.
故选:A.

练习册系列答案
相关题目