题目内容
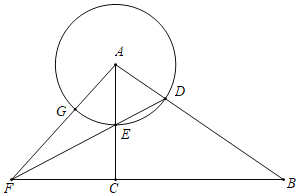
【题目】在Rt△ABC中,∠ACB=90°,AC=15,sin∠BAC=![]() .点D在边AB上(不与点A、B重合),以AD为半径的⊙A与射线AC相交于点E,射线DE与射线BC相交于点F,射线AF与⊙A交于点G.
.点D在边AB上(不与点A、B重合),以AD为半径的⊙A与射线AC相交于点E,射线DE与射线BC相交于点F,射线AF与⊙A交于点G.
(1)如图,设AD=x,用x的代数式表示DE的长;
(2)如果点E是![]() 的中点,求∠DFA的余切值;
的中点,求∠DFA的余切值;
(3)如果△AFD为直角三角形,求DE的长.
【答案】(1)![]() ;(2)∠DFA的余切值为
;(2)∠DFA的余切值为![]() ;(3)DE的长为
;(3)DE的长为![]() 或
或![]() .
.
【解析】
(1)过点D作DH⊥AC,垂足为H.根据锐角三角函数和勾股定理即可用x的代数式表示DE的长;
(2)根据题意可设BC=4k(k>0),AB=5k,则AC=![]() =3k.过点A作AM⊥DE,垂足为M,再根据锐角三角函数和勾股定理即可表示∠DFA的余切值;
=3k.过点A作AM⊥DE,垂足为M,再根据锐角三角函数和勾股定理即可表示∠DFA的余切值;
(3)分两种情况讨论:当点E在AC上时,只有可能∠FAD=90°;当点E在AC的延长线上时,只有可能∠AFD=90°,此时∠AFC=∠AEF.根据锐角三角函数和勾股定理即可求DE的长.
解:(1)如图,
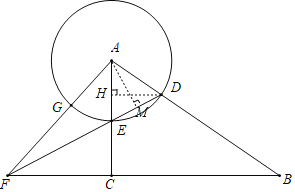
过点D作DH⊥AC,垂足为H.
在Rt△AEH中,![]() ,
,
![]() .
.
在⊙A中,AE=AD=x,
∴![]() ,
,
∴![]() ;
;
(2)∵![]() ,
,
∴可设BC=4k(k>0),AB=5k,
则AC=![]() =3k.
=3k.
∵AC=15,
∴3k=15,
∴k=5.
∴BC=20,AB=25.
∵点E是![]() 的中点,由题意可知此时点E在边AC上,点F在BC的延长线上,
的中点,由题意可知此时点E在边AC上,点F在BC的延长线上,
∴∠FAC=∠BAC.
∵∠FCA=∠BCA=90°,AC=AC,
∴△FCA≌△BCA(ASA),
∴FC=BC=20.
∵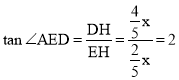 ,
,
又∵∠AED=∠FEC,且∠AED、∠FEC都为锐角,
∴tan∠FEC=2.
∴![]() .
.
∴AE=AC﹣EC=15﹣10=5.
过点A作AM⊥DE,垂足为M,
则![]() .
.
∵ ,
,
∴![]() .
.
在Rt△EFC中,![]() .
.
∴在Rt△AFM中,![]() .
.
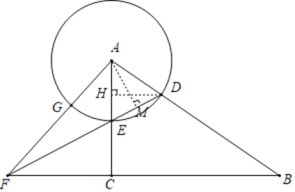
答:∠DFA的余切值为![]() ;
;
(3)当点E在AC上时,只有可能∠FAD=90°.
∵FC=CEtan∠FEC=2(15﹣x),
∴![]() .
.
∴![]() .
.
∵![]() ,
,
又∵∠AED=∠ADE,且∠AED、∠ADE都为锐角,
∴![]() .
.
∴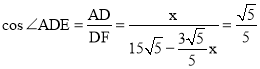 .
.
∴AD=x=![]() .
.
∴![]() .
.
当点E在AC的延长线上时,只有可能∠AFD=90°,
![]()
![]()
![]() ∠AFC=∠AEF.
∠AFC=∠AEF.
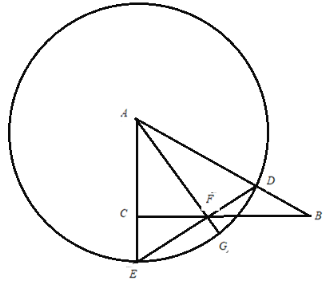
∵∠AFC、∠AEF都为锐角,
∴tan∠AEF=tan∠AFC=2.
∵CE=AE﹣AC=x﹣15,
∴CF=CEtan∠AEF=2(x﹣15).
∴![]() .
.
∴AD=x=![]() .
.
∴.
综上所述,△AFD为直角三角形时,DE的长为![]() 或
或![]() .
.