题目内容
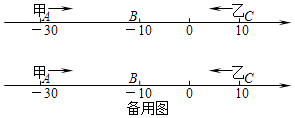
【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,动点P从A点出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t<0)秒. ![]()
(1)写出数轴上点B表示的数;点P表示的数(用含t的代数式表示)
(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向右匀速运动,若点P,Q同时出发,问多少秒时P,Q之间的距离恰好等于2?
(3)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速到家动,若点P,Q同时出发,问多少秒时P,Q之间的距离恰好又等于2?
(4)若M为AP的中点,N为BP的中点,在点P运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由,若不变,请他画出图形,并求出线段MN的长.
【答案】
(1)﹣12;8﹣5t
(2)解:若点P、Q同时出发,设t秒时P、Q之间的距离恰好等于2.分两种情况:
①点P、Q相遇之前,
由题意得3t+2+5t=20,解得t=2.25;
②点P、Q相遇之后,
由题意得3t﹣2+5t=20,解得t=2.75.
答:若点P、Q同时出发,2.25或2.75秒时P、Q之间的距离恰好等于2
(3)解:设点P运动x秒时,P、Q之间的距离恰好等于2.分两种情况:
①点P、Q相遇之前,
则5x﹣3x=20﹣2,
解得:x=9;
②点P、Q相遇之后,
则5x﹣3x=20+2
解得:x=11.
答:若点P、Q同时出发,9或11秒时P、Q之间的距离恰好又等于2
(4)解:线段MN的长度不发生变化,都等于10;理由如下:
① 当点P在点A、B两点之间运动时:
![]()
MN=MP+NP= ![]() AP+
AP+ ![]() BP=
BP= ![]() (AP+BP)=
(AP+BP)= ![]() AB=
AB= ![]() ×20=10,
×20=10,
②当点P运动到点B的左侧时:
![]()
MN=MP﹣NP= ![]() AP﹣
AP﹣ ![]() BP=
BP= ![]() (AP﹣BP)=
(AP﹣BP)= ![]() AB=10,
AB=10,
则线段MN的长度不发生变化,其值为10
【解析】解:(1)数轴上点B表示的数为8﹣20=﹣12;点P表示的数为8﹣5t; 所以答案是:﹣12;8﹣5t.
【考点精析】掌握数轴和两点间的距离是解答本题的根本,需要知道数轴是规定了原点、正方向、单位长度的一条直线;同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案