题目内容
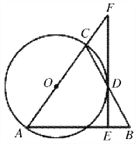
【题目】如图，在△ABC中，AB=AC，以AC为直径作
交BC于点D，过点D作FE⊥AB于点E，交AC的延长线于点F.
(1)求证: EF与相切；
(2)若AE=6，
，求EB的长.
【答案】(1)见解析（2）
【解析】分析：（1）如图，欲证明EF与⊙O相切，只需证得OD⊥EF．
（2）通过解直角△AEF可以求得AF=10．设⊙O的半径为r，由平行线分线段成比例得到
，即
，则易求AB=AC=2r=
，所以EB=AB﹣AE=﹣6=．
详解：（1）证明：如图，连接OD．
∵OC=OD，∴∠OCD=∠ODC．
∵AB=AC，∴∠ACB=∠B，∴∠ODC=∠B，∴OD∥AB，∴∠ODF=∠AEF．
∵EF⊥AB，∴∠ODF=∠AEF=90°，∴OD⊥EF．
∵OD是⊙O的半径，∴EF与⊙O相切；
（2）由（1）知，OD∥AB，OD⊥EF．
在Rt△AEF中，sin∠CFD=
，AE=6，则AF=10．
∵OD∥AB，∴．
设⊙O的半径为r，∴，解得：r=
，∴AB=AC=2r=，∴EB=AB﹣AE=﹣6=．
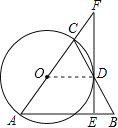
【题目】缴纳个人所得税是收入达到缴纳标准的公民应居的义务，个人所得税率是由国家相应的法律法规规定的.根据个人的收入计算，新修改的《中华人民共和国个人所得税法》于2019年1月1日正式实施，新税法规定个人所得税的免征额为5000元，应纳税所得额按如下税率表缴纳个人所得税(应纳税所得额＝税前收总额﹣国家规定扣除专项金额﹣免征额).
级数 | 应纳税所得额 | 税率% |
1 | 不超过3000元的 | 3 |
2 | 超过3000元至12000元的部分 | 10 |
3 | 超过12000元至25000元的部分 | 20 |
… | … | … |
根据以上信息，解决以下问题：
(1)小明的妈妈应纳税所得额为2000元，她应该缴纳个人所得税______元.
(2)小明的爸爸要缴纳个人所得税590元，他应纳税所得额是多少元？
(3)如果小明的爸爸和妈妈某月应纳税所得额共为20000元(爸爸的应纳税所得额高于妈妈的应纳税所得额)，共要缴纳个人所得税1780元，小明的爸爸应纳税所得额是_____元.
【题目】观察下表：
序号 | 1 | 2 | 3 | …… |
x x x x | ||||
x x x | y y y | |||
x x | y y | x x x x | ||
图形 | y | x x x | y y y | |
x x | y y | x x x x | ||
x x x | y y y | |||
x x x x |
我们把某格中字母和所得到的多项式称为“特征式多项式”。例如第1格的“特征式多项式”为4x＋y。
（1）第3格的“特征式多项式”为________________；
（2）第4格的“特征式多项式”为________________；
（3）第n格的“特征式多项式”为________________；
（4）若第1格的 “特征式多项式”为10，第2格的“特征式多项式”为19，求x、y的值。
