Question

【题目】如图所示，在△ABC中，BO、CO是角平分线．

（1）∠ABC=50°，∠ACB=60°，求∠BOC的度数，并说明理由．

（2）题（1）中，如将“∠ABC=50°，∠ACB=60°”改为“∠A=70°”，求∠BOC的度数．

（3）若∠A=n°，求∠BOC的度数．

Answer 1

【答案】（1）125°；（2）125°；（3）∠BOC=90°+n°．

【解析】

如图，由BO、CO是角平分线得∠ABC=2∠1，∠ACB=2∠2，再利用三角形内角和得到∠ABC+∠ACB+∠A=180°，则2∠1+2∠2+∠A=180°，接着再根据三角形内角和得到∠1+∠2+∠BOC=180°，利用等式的性质进行变换可得∠BOC=90°+∠A，然后根据此结论分别解决（1）、（2）、（3）．

如图，

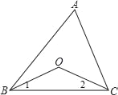
∵BO、CO是角平分线，

∴∠ABC=2∠1，∠ACB=2∠2，

∵∠ABC+∠ACB+∠A=180°，

∴2∠1+2∠2+∠A=180°，

∵∠1+∠2+∠BOC=180°，

∴2∠1+2∠2+2∠BOC=360°，

∴2∠BOC﹣∠A=180°，

∴∠BOC=90°+∠A，

（1）∵∠ABC=50°，∠ACB=60°，

∴∠A=180°﹣50°﹣60°=70°，

∴∠BOC=90°+×70°=125°；

（2）∠BOC=90°+∠A=125°；

（3）∠BOC=90°+n°．