题目内容
△ABC中，AB=15，AC=13，高AD=12，则△ABC的周长是______．
此题应分两种情况说明：
（1）当△ABC为锐角三角形时，在Rt△ABD中，
BD=
=
=9，
在Rt△ACD中，
CD=
=
=5
∴BC=5+9=14
∴△ABC的周长为：15+13+14=42；
（2）当△ABC为钝角三角形时，
在Rt△ABD中，BD=
=
=9，
在Rt△ACD中，CD=
=
=5，
∴BC=9-5=4．
∴△ABC的周长为：15+13+4=32
∴当△ABC为锐角三角形时，△ABC的周长为42；当△ABC为钝角三角形时，△ABC的周长为32．
综上所述，△ABC的周长是42或32．
故填：42或32．
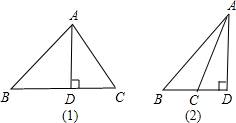
（1）当△ABC为锐角三角形时，在Rt△ABD中，
BD=
| AB2-AD2 |
| 152-122 |
在Rt△ACD中，
CD=
| AC2-AD2 |
| 132-122 |
∴BC=5+9=14
∴△ABC的周长为：15+13+14=42；
（2）当△ABC为钝角三角形时，
在Rt△ABD中，BD=
| AB2-AD2 |
| 152-122 |
在Rt△ACD中，CD=
| AC2-AD2 |
| 132-122 |
∴BC=9-5=4．
∴△ABC的周长为：15+13+4=32
∴当△ABC为锐角三角形时，△ABC的周长为42；当△ABC为钝角三角形时，△ABC的周长为32．
综上所述，△ABC的周长是42或32．
故填：42或32．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
