Question

【题目】如图①，在 中，，平分的外角，与的垂直平分线相交于点，连结．

（1）求证：；

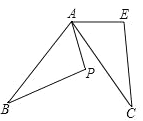
（2）如图②，的角平分线与中线相交于点，若，，，则 ．（直接填数值）

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）连接AH交BC于点O，过点H作HQ⊥BC于点Q，作HP⊥AC交AC的延长线于点P，利用HL证出Rt△BHQ≌Rt△AHP，再利用三角形外角的性质即可得出结论；

（2）过点E作ED⊥BC于D，连接AN，根据勾股定理的逆定理即可判断△ABC为直角三角形，∠BAC=90°，然后根据勾股定理即可求出ED，再结合等高时，面积比等于底之比即可推出结论．

解：（1）连接AH交BC于点O，过点H作HQ⊥BC于点Q，作HP⊥AC交AC的延长线于点P

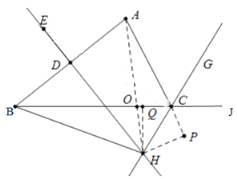
∵HE垂直平分AB

∴BH=AH

∴∠ABH=∠HAB

∵平分的外角

∴CH平分∠QCP

∴HQ=HP，∠QCP =2∠BCH

在Rt△BHQ和Rt△AHP中

∴Rt△BHQ≌Rt△AHP

∴∠HBQ=∠HAP

∵∠QCP=∠CAB＋∠CBA=∠HAB＋∠HAP＋∠CBA=∠HAB＋∠HBQ＋∠CBA=∠HAB＋∠ABH=2∠ABH

∴∠ABH=∠BCH

（2）过点E作ED⊥BC于D，连接AN

∵，

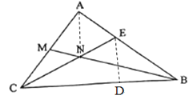
∴△ABC为直角三角形，∠BAC=90°

∵CE平分∠ACB

∴AE=ED，∠ACE=∠DCE

∴∠AEC=90°－∠ACE=90°－∠DCE=∠DEC

∴AC=CD=6

∴BD=BC－CD=4

设AE=ED=x，则BE=AB－AE=8－x

在Rt△EDB中，ED2＋BD2=BE2

x2＋42=（8－x）2

解得：x=3,

即AE=ED=3，BE=5

S△ABC=AC·AB=24

∴S△ACE=·S△ABC=×24=9，S△BCE=·S△ABC=×24=15

∵点M为AC的中点

∴S△BCM=S△ABC=12，S△NAM=S△NCM，

设S△NAM=S△NCM=S，

∴S△ANE=S△ACE－S△NAM－S△NCM=9－2S，S△BCN=S△BCM－S△NCM=12－S

∴S△NBE= S△BCE－S△BCN=3＋S

∵

∴

解得：

∴S△ACN=2S=，S△ANE= 9－2S=

∴

∴

故答案为：．