��Ŀ����
����Ŀ�����Ǹ������¶��壺˳����������һ���ı��θ����е����õ��ı��ν��е��ı��Σ�
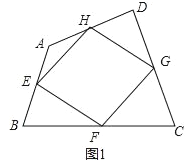
��1����ͼ1���ı���ABCD�У���E��F��G��H�ֱ�Ϊ��AB��BC��CD��DA���е㣮��֤���е��ı���EFGH��ƽ���ı��Σ�
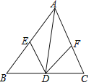
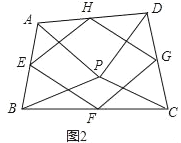
��2����ͼ2����P���ı���ABCD��һ�㣬������PA=PB��PC=PD����APB=��CPD����E��F��G��H�ֱ�Ϊ��AB��BC��CD��DA���е㣬�����е��ı���EFGH����״����֤����IJ��룻
��3�����ı䣨2���е�������ʹ��APB=��CPD=90���������������䣬ֱ��д���е��ı���EFGH����״����֤����IJ��룮
���𰸡���1������������2���ı���EFGH����������3���ı���EFGH��������.
����������������1����ͼ1�У�����BD��������������λ�߶���ֻҪ֤��EH��FG��EH=FG���ɣ�
��2���ı���EFGH�����Σ���֤����APC�ա�BPD���õ�AC=BD����֤��EF=FG���ɣ�
��3���ı���EFGH�������Σ�ֻҪ֤����EHG=90����������APC�ա�BPD���á�ACP=��BDP������֤����COD=��CPD=90�����ٸ���ƽ���ߵ����ʼ���֤����
��⣺��1����ͼ1������BD��
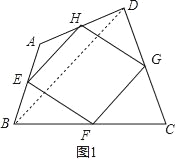
�ߵ�E��H�ֱ�Ϊ��AB��AD���е㣬
��EH��BD��EH=![]() BD��
BD��
�ߵ�F��G�ֱ�ΪBC��DC���е㣬
��FG��BD��FG=![]() BD��
BD��
��EH=FG��EH��FG��
���е��ı���EFGH��ƽ���ı��Σ�
��2���ı���EFGH�����Σ�
��ͼ2������AC��BD��
�ߡ�APB=��CPD��
���APB+��APD=��CPD+��APD������APC=��BPD��
�ڡ�APC�͡�BPD�У�
AP=BP����APC=��BPD��PC=PD��
���APC�ա�BPD��SAS����
��AC=BD��
�ߵ�E��F��G�ֱ�ΪAB��BC��CD���е㣬
��EF=![]() AC��FG=
AC��FG=![]() BD��
BD��
��EF=FG��
���ı���EFGH��ƽ���ı��Σ�
���ı���EFGH�����Σ�
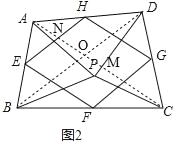
��3���ı���EFGH�������Σ�
��AC��BD����ΪO��AC��PD���ڵ�M��AC��EH���ڵ�N��
�ߡ�APC�ա�BPD��
���ACP=��BDP��
�ߡ�DMO=��CMP��
���COD=��CPD=90�㣬
��EH��BD��AC��HG��
���EHG=��ENO=��BOC=��DOC=90�㣬
���ı���EFGH�����Σ�
���ı���EFGH�������Σ�

 �����Ƹ���ʦ����ϵ�д�
�����Ƹ���ʦ����ϵ�д� ��ͨ����ͬ����ϰ��ϵ�д�
��ͨ����ͬ����ϰ��ϵ�д�