题目内容
【题目】如图,在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD.AG. 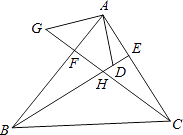
(1)求证:AD=AG;
(2)AD与AG的位置关系如何.
【答案】
(1)解:∵BE、CF分别是AC、AB两边上的高,
∴∠AFC=∠BFC=∠BEC=∠BEA=90°
∴∠BAC+∠ACF=90°,∠BAC+∠ABE=90°,∠G+∠GAF=90°,
∴∠ABE=∠ACF.
在△ABD和△GCA中,
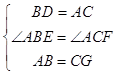 ,
,
∴△ABD≌△GCA(SAS),
∴AD=GA,
(2)解:结论:AG⊥AD.
理由:∵△ABD≌△GCA(SAS),
∴∠BAD=∠G,
∴∠BAD+∠GAF=90°,
∴AG⊥AD.
【解析】(1)先由条件可以得出∠ABE=∠ACF,就可以得出△ABD≌△GCA,就有AD=GA,∠BAD=∠G;(2)结论:AG⊥AD.由(1)可以得出∠GAD=90°,进而得出AG⊥AD.

练习册系列答案
相关题目