题目内容
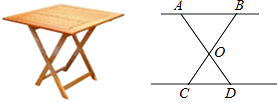
【题目】如图,四边形ABCD的对角线AC和BD交于点O,则下列不能判断四边形ABCD是平行四边形的条件是( ) 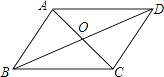
A.OA=OC,AD∥BC
B.∠ABC=∠ADC,AD∥BC
C.AB=DC,AD=BC
D.∠ABD=∠ADB,∠BAO=∠DCO
【答案】D
【解析】解:A、∵AD∥BC, ∴∠ADB=∠CBD,
在△BOC和△DOA中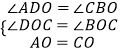 ,
,
∴△BOC≌△DOA(AAS),
∴BO=DO,
∴四边形ABCD是平行四边形,正确,故本选项错误;
B、∵∠ABC=∠ADC,AD∥BC,
∴∠ADC+∠DCB=180°,
∴∠ABC+∠BCD=180°,
∴AB∥DC,
∴四边形ABCD是平行四边形,正确,故本选项错误;
C、∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,正确,故本选项错误;
D、由∠ABD=∠ADB,∠BAO=∠DCO,
无法得出四边形ABCD是平行四边形,错误,故本选项正确;
故选:D.
【考点精析】掌握平行四边形的判定是解答本题的根本,需要知道两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目