题目内容
【题目】如图,过原点的直线![]() 和
和![]() 与反比例函数
与反比例函数![]() 的图象分别交于两点
的图象分别交于两点![]() 和
和![]() ,连结
,连结![]() .
.
(1)四边形![]() 一定是什么四边形;(直接写结果)
一定是什么四边形;(直接写结果)
(2)四边形![]() 可能是矩形吗?若可能,求此时
可能是矩形吗?若可能,求此时![]() 和
和![]() 之间的关系式;若不可能,说明理由;
之间的关系式;若不可能,说明理由;
(3)设![]() 是函数
是函数![]() 图象上的任意两点,
图象上的任意两点,![]() ,请判断
,请判断![]() 的大小关系,并说明理由.
的大小关系,并说明理由.
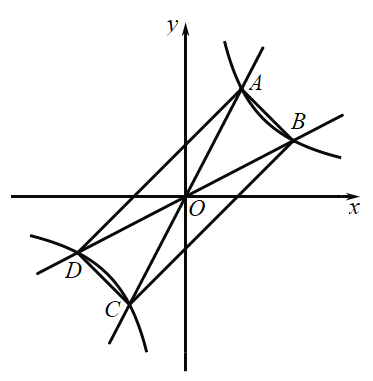
【答案】(1)平行四边形;(2)可能,k1k2=1;(3)a>b,见解析
【解析】
(1)根据直线![]() 和
和![]() 与反比例函数
与反比例函数![]() 的图像关于原点对称,即可确定;
的图像关于原点对称,即可确定;
(2)联立方程求得A、B点的坐标,然后根据OA=OB,依据勾股定理得出![]() ,两边平分得
,两边平分得![]() ,整理后得(k1-k2)(k1k2-1)=0,根据k1≠k2,则k1k2-1=0,即可解答;
,整理后得(k1-k2)(k1k2-1)=0,根据k1≠k2,则k1k2-1=0,即可解答;
(3)由(x1,y1),Q(x2,y2)(x2>x1>0)是函数图像上的任意两点,可得![]() ,求出
,求出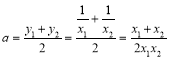 ,得到
,得到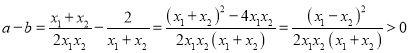 即可解答.
即可解答.
解:(1)∵直线![]() 和
和![]() 与反比例函数
与反比例函数![]() 的图像关于原点对称,
的图像关于原点对称,
∴OA=OC,OB=OD
∴四边形ABCD是平行四边形
(2)若四边形ABCD是矩形时,OA=OB
设A(x’,y’), 则y’=k1x’, y’=1/x’得x’2=![]()
∴OA2 = x’2 + y’2 =![]() + k1,同理OB2=
+ k1,同理OB2=![]() + k2,
+ k2,
∴![]() + k1 =
+ k1 =![]() + k2 ,得(k1 –k2)(
+ k2 ,得(k1 –k2)(![]() - 1)= 0
- 1)= 0
∵k2 – k1 ≠ 0, ∴![]() – 1 = 0
– 1 = 0
∴k1k2=1
所以四边形ABCD可以是矩形,此时k1k2=1
(3)∵由(x1,y1),Q(x
∴![]()
∴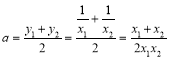
∵![]()
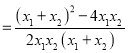
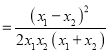
∵x2 > x1 > 0,
∴(x1– x2)2 > 0,2x1x2 (x1+ x2)> 0
∴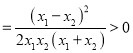
∴a > b

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目