题目内容
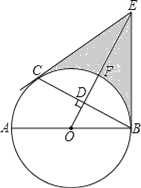
【题目】如图,将等腰△ABC绕顶点B逆时针方向旋转40°得到△A1BC1,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E、F.

求证:ΔBCF≌ΔBA1D.
当∠C=40°时,请你证明四边形A1BCE是菱形.
【答案】(1)详见解析;(2)详见解析.
【解析】试题分析:(1)根据旋转的性质,得出A1B=AB=BC,∠A=∠A1=∠C,∠A1BD=∠CBC1,再根据ASA即可判定△BCF≌△BA1D;
(2)根据∠C=40°,△ABC是等腰三角形,即可得出∠A=∠C1=∠C=40°,进而得到∠C1=∠CBF,∠A=∠A1BD,由此可判定A1E∥BC,A1B∥CE,进而得到四边形A1BCE是平行四边形,最后根据A1B=BC,即可判定四边形A1BCE是菱形.
(1)∵△ABC是等腰三角形,
∴AB=BC,∠A=∠C,
∵将等腰△ABC绕顶点B逆时针方向旋转40度到△A1BC1的位置,
∴A1B=AB=BC,∠A=∠A1=∠C,∠A1BD=∠CBC1,
在△BCF与△BA1D中,  ,
,
∴△BCF≌△BA1D(ASA);
(2)∵∠C=40°,△ABC是等腰三角形,
∴∠A=∠C1=∠C=40°,
∴∠C1=∠CBF=40°,∠A=∠A1BD=40°,
∴A1E∥BC,A1B∥CE,
∴四边形A1BCE是平行四边形,
∵A1B=BC,
∴四边形A1BCE是菱形.

【题目】某小型企业实行工资与业绩挂钩制度,工人工资分为A、B、C、D四个档次.小明对该企业三月份工人工资进行调查,并根据收集到的数据,绘制了如下尚不完整的统计表与扇形统计图.
档次 | 工资(元) | 频数(人) | 频率 |
A | 3000 | 20 | |
B | 2800 | 0.30 | |
C | 2200 | ||
D | 2000 | 10 |
根据上面提供的信息,回答下列问题:
(1)求该企业共有多少人?
(2)请将统计表补充完整;
(3)扇形统计图中“C档次”的扇形所对的圆心角是 度.