题目内容
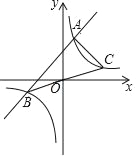
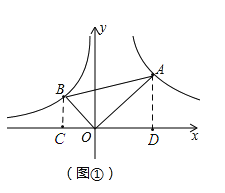
【题目】如图①,已知点A在反比例函数![]() (x>0)的图像上,点B在经过点(-2,1)的反比例函数
(x>0)的图像上,点B在经过点(-2,1)的反比例函数![]() (x<0)的图像上,连结OA,OB,AB.
(x<0)的图像上,连结OA,OB,AB.

(1)求k的值;
(2)若∠AOB=90°,求∠OAB的度数;
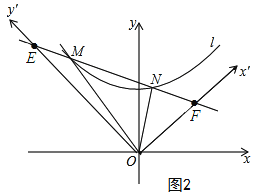
(3)将反比例函数![]() (x>0)的图像绕坐标原点O逆时针旋转45°得到曲线l,过点E
(x>0)的图像绕坐标原点O逆时针旋转45°得到曲线l,过点E![]() ,F
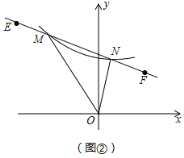
,F![]() 的直线与曲线l相交于点M,N,如图②所示,求△OMN的面积.
的直线与曲线l相交于点M,N,如图②所示,求△OMN的面积.
【答案】(1)-2;(2)30°;(3)8
【解析】
(1)把点(-2,1)代入反比例函数![]() 即可求出k的值;
即可求出k的值;
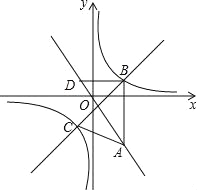
(2)过点B作BC⊥x轴,过点A作AD⊥x轴,设点B(a,-![]() ),点A(b,
),点A(b,![]() )设点B(a,-
)设点B(a,-![]() ),点A(b,
),点A(b,![]() )则CO=-a,BC=-
)则CO=-a,BC=-![]() ,AD=
,AD=![]() ,OD=b,证得△BCO∽△ODA故
,OD=b,证得△BCO∽△ODA故![]()
得出ab=-2![]() ,求得 tan∠BAO=
,求得 tan∠BAO=![]() ,故∠BAO=30°;
,故∠BAO=30°;
(3)由点E![]() ,F
,F![]() ,得OE⊥OF建立新的坐标系,OF为x’轴,OE为y’轴,在新的坐标系中,E(0,8),F(4,0)求得直线EF的解析式为y’=-2x’+8,联立两函数解得M(1,6),N(3,2),即可求出△OMN的面积.
,得OE⊥OF建立新的坐标系,OF为x’轴,OE为y’轴,在新的坐标系中,E(0,8),F(4,0)求得直线EF的解析式为y’=-2x’+8,联立两函数解得M(1,6),N(3,2),即可求出△OMN的面积.
(1)∵把点(-2,1)代入反比例函数![]() (x<0),
(x<0),
∴k=-2×1=-2,
(2)如图,过点B作BC⊥x轴,过点A作AD⊥x轴,
设点B(a,-![]() ),点A(b,
),点A(b,![]() )
)
∴CO=-a,BC=-![]() ,AD=
,AD=![]() ,OD=b
,OD=b
∵∠AOB=90°,
∴∠BOC+∠AOD=90°,且∠BOC+∠CBO=90°,
∴∠AOD=∠CBO,且∠BCO=∠ADO=90°
∴△BCO∽△ODA
∴![]()
∴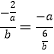
∴ab=-2![]()
∴![]()
∴tan∠BAO=![]()
∴∠BAO=30°
(3)∵点E![]() ,F
,F![]()
∴OE⊥OF
建立如图2新的坐标系,OF为x’轴,OE为y’轴,
在新的坐标系中,E(0,8),F(4,0)代入y’=kx’+b
求得直线EF的解析式为y’=-2x’+8
由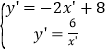
解得![]() 或
或![]()
∴M(1,6),N(3,2)
∴S△OMN= S△OFM- S△OFN=![]()