��Ŀ����
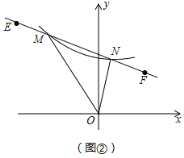
����Ŀ����ƽ��ֱ������ϵxoy�У���M��x����������ϣ���M��x����A��B���㣬��y��C��D�����㣬��CΪ��AE���е㣬AE��y���ڵ�G�㣬����C������Ϊ��0��2![]() ����
����
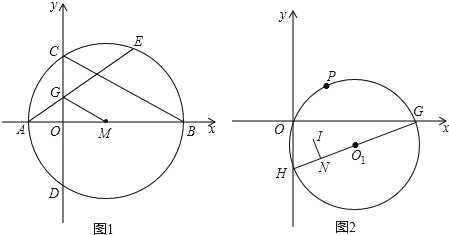
��1������MG��BC����֤��MG��BC��
��2����CE��AB��ֱ��y��kx��1��k��0�����ı���ACEB������ȷ֣���k��ֵ��
��3����ͼ2����O��P��2��2������O1��x����������G����y�Ḻ������H��IΪ��GOH�����ģ���I��IN��GH��N������O1�Ĵ�С�仯ʱ����˵��GN��NH��ֵ���䲢����ֵ��
���𰸡���1��֤������������2��![]() ����3��֤����������GN��NH��ֵΪ4
����3��֤����������GN��NH��ֵΪ4
��������
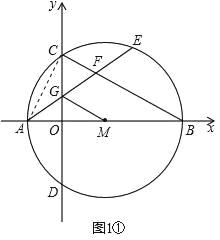
��1������AC����AE��BC�Ľ���ΪF����ͼ1�٣������֪AM��BM��Ҫ֤MG��BC��ֻ��֤AG��FG�����ڡ�ACF��90����ֻ��֤AG��CG���ɣ�
��2������AC��CE��BE����AE��BC�Ľ���ΪF��ֱ��y��kx��1��CE����P����AB����Q����ͼ1�ڣ�������CE��AB�������ACO�Ķ��������������CE��AB�ij�����k�Ĵ���ʽ��ʾ��CP��AQ�ij��ȣ�Ȼ����������г�����k�ķ��̣��Ϳ����k��ֵ��
��3������I��IA��OH��A����IB��OG��B������P��PC��y����C����PD��x����D������IO��IH��IG��PH��PG����ͼ2�����ݽ�ƽ���ߵ����ʿɵ�IA��IB��IN�����ù��ɶ����ɵ�AH��NH��GN��GB��OA��OB���Ӷ��ɵ�GN��NH��OG��OH����֤����OCPD�������Σ��Ӷ��С�CPD��90����PC��PD��������֤����PCH�ա�PDG������CH��DG����CO+OH��OG��OD���Ӷ���OG��OH��4�������ɵ�GN��NH��OG��OH��4��������Խ����
�⣺��1������AC����AE��BC�Ľ���ΪF����ͼ1�٣�
��AB�ǡ�M��ֱ����AB��CD��
���ACB��90����![]() ��
��
��![]() ��
��
��![]() ��
��
���ACD����CAE��
��GA��GC����GCF��90������ACD��90������CAE����CFG��
��GC��GF��
��AG��GF��
��AM��BM��
��MG��BC��
��2������AC��CE��BE����AE��BC�Ľ���ΪF��ֱ��y��kx��1��CE����P����AB����Q����ͼ1�ڣ�
��CE��AB�����CEA����BAE��
��![]() �����CAE����CEA��
�����CAE����CEA��
���ACO����CAE����GAO��
�ߡ�AOC��90����
��3��ACO��90����
���ACO��30����
�ߵ�C������Ϊ��0��2![]() ����
����
��OC��2![]() ��
��
��A0��OCtan��ACO��2![]() ��
��![]() ��2��
��2��
���A����������2��0����AC��2AO��4��
��![]() ��
��
��EC��AC��4����ABC����CAE��30����
��AB��2AC��8��
��yQ��0��
��kxQ��1��0����xQ��![]() ��
��
��AQ��![]() ������2����
������2����![]() +2��
+2��
�ߵ�C������Ϊ��0��2![]() ����CE��AB��
����CE��AB��
��yP��2![]() ��
��
��kxP��1��2![]() ����xP��
����xP��![]() ��
��
��CP��![]() ��
��
��S����ACPQ��![]() S����ABEC��
S����ABEC��
��![]() ��CP+AQ��OC��
��CP+AQ��OC��![]() ��
��![]() ��CE+AB��OC��
��CE+AB��OC��
��2��CP+AQ����CE+AB��
��2��![]() +
+![]() +2����4+8��12��
+2����4+8��12��
��ã�k��![]() ��
��
������k��![]() ��ԭ���̵Ľ⣮
��ԭ���̵Ľ⣮
��k��ֵΪ![]() ��
��

��3������I��IA��OH��A����IB��OG��B������P��PC��y����C����
PD��x����D������IO��IH��IG��PH��PG����ͼ2��
�ߵ�I����GOH�����ģ�
���I����GOH���ڽ�ƽ���ߵĽ��㣮
��IA��OH��IB��OG��IN��GH��
��IA��IB��IN��
��AH��![]() ��
��![]() ��NH��
��NH��
ͬ��GN��GB��OA��OB��
��GN��NH��GB��AH����OG��OB������OH��OA����OG��OH��
��P��������2��2����
��OD��OC��2��
��PC��OC��PD��OD��OC��OD��
���PCO����COD����PDO��90����
���ı���OCPD�Ǿ��Σ�
��OD��OC��
�����OCPD��������
���CPD��90����PC��PD��
��GH�ǡ�O1ֱ����
���GPH��90����
���CPD����GPH��
���CPH����DPG��
���PCH�ա�PDG��ASA����
��CH��DG��
��CO+OH��OG��OD��
��2+OH��OG��2��
��OG��OH��4��
��GN��NH��OG��OH��4��
��GN��NH��ֵ���䣬��ֵΪ4��

 ���㼤�������100�ִ��Ծ�ϵ�д�
���㼤�������100�ִ��Ծ�ϵ�д�����Ŀ��6��14������������Ѫ������ij�в�ȡ��Ը�����ķ�ʽ��֯����������Ѫ����ѪʱҪ����Ѫ�ߵ�Ѫ�ͽ��м�⣬���������A��������B��������AB��������O����4�����ͣ�����Ѫ����Ⱥ�У������ȡ�˲�����Ѫ�ߵ�Ѫ�ͽ������ͳ�ƣ����������ͳ�ƽ��������������������ͼ����
Ѫ�� | A | B | AB | O |
���� | �� �� | 10 | 5 | �� �� |
��1����������ȡ����Ѫ������Ϊ�� ���ˣ�m=�� ����
��2����ȫ�ϱ��е����ݣ�
��3������λ�и�����3000��������Ѫ��������ݳ�������ش�
����Ѫ����Ⱥ���γ�ȡһ�ˣ���Ѫ����A�͵ĸ����Ƕ��٣���������3000���д�Լ�ж�������A��Ѫ��