题目内容
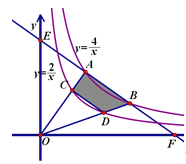
【题目】如图,在平面直角坐标系xOy中,点A(a,﹣![]() )在直线y=﹣
)在直线y=﹣![]() 上,AB∥y轴,且点B的纵坐标为1,双曲线y=
上,AB∥y轴,且点B的纵坐标为1,双曲线y=![]() 经过点B.
经过点B.
(1)求a的值及双曲线y=![]() 的解析式;
的解析式;
(2)经过点B的直线与双曲线y=![]() 的另一个交点为点C,且△ABC的面积为
的另一个交点为点C,且△ABC的面积为![]() .
.
①求直线BC的解析式;
②过点B作BD∥x轴交直线y=﹣![]() 于点D,点P是直线BC上的一个动点.若将△BDP以它的一边为对称轴进行翻折,翻折前后的两个三角形所组成的四边形为正方形,直接写出所有满足条件的点P的坐标.
于点D,点P是直线BC上的一个动点.若将△BDP以它的一边为对称轴进行翻折,翻折前后的两个三角形所组成的四边形为正方形,直接写出所有满足条件的点P的坐标.
【答案】(1)y=![]() (2)①y=x-1②(﹣1,﹣2)或(
(2)①y=x-1②(﹣1,﹣2)或(![]() ,-
,-![]() )
)
【解析】
试题(1)根据一次函数图象上点的坐标特征可得到![]() 解得a=2,则A(2,-
解得a=2,则A(2,-![]() )),再确定点B的坐标为(2,1),然后把B点坐标代入
)),再确定点B的坐标为(2,1),然后把B点坐标代入![]() 中求出m的值即可得到反比例函数的解析式;
中求出m的值即可得到反比例函数的解析式;
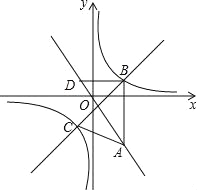
(2)①过点C作CE⊥AB于点E,如图5.,根据三角形面积公式得到![]() 解得CE=3,点C的横坐标为-1.
解得CE=3,点C的横坐标为-1.
∵点C在双曲线![]() 上,则点C的坐标为(-1,-2),再利用待定系数法求直线BC的解析式;②先确定D(-1,1),根据直线BC解析式的特征可得直线BC与x轴的夹角为45°,而BD∥x轴,于是得到∠DBC=45°,根据正方形的判定方法,只有△PBD为等腰直角三角形时,以它的一边为对称轴进行翻折,翻折前后的两个三角形所组成的四边形为正方形,分类讨论:若∠BPD=90°,则点P在BD的垂直平分线上,易得此时P(
上,则点C的坐标为(-1,-2),再利用待定系数法求直线BC的解析式;②先确定D(-1,1),根据直线BC解析式的特征可得直线BC与x轴的夹角为45°,而BD∥x轴,于是得到∠DBC=45°,根据正方形的判定方法,只有△PBD为等腰直角三角形时,以它的一边为对称轴进行翻折,翻折前后的两个三角形所组成的四边形为正方形,分类讨论:若∠BPD=90°,则点P在BD的垂直平分线上,易得此时P(![]() ,-
,-![]() );若∠BDP=90°,利用PD∥y轴,易得此时P(-1,-2).
);若∠BDP=90°,利用PD∥y轴,易得此时P(-1,-2).
试题解析:(1)∵点A![]() 在直线
在直线![]() 上,
上,
∴![]() .
.
∴![]() .…………………………1分
.…………………………1分
∵AB∥y轴,且点B的纵坐标为1,
∴点B的坐标为(2,1).
∵双曲线![]() 经过点B(2,1),
经过点B(2,1),
∴![]() ,即
,即![]() .
.
∴反比例函数的解析式为![]() .
.
(2)①过点C作CE⊥AB于点E,如图.
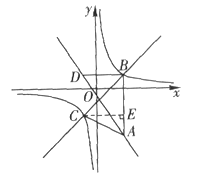
∴![]() .
.
∴CE="3."
∴点C的横坐标为-1.
∵点C在双曲线![]() 上,
上,
∴点C的坐标为(-1,-2).
设直线BC的解析式为![]() ,
,
则![]() 解得
解得![]()
∴直线BC的解析式为![]() .
.
②(-1,-2)或![]() .
.

 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案