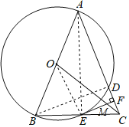
题目内容
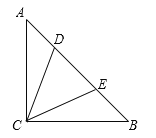
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的
为直径的![]() 交边
交边![]() 于点
于点![]() (点
(点![]() 不与点
不与点![]() 重合),交边
重合),交边![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() .
.
①求![]() 的半径;
的半径;
②连接![]() 交
交![]() 于点
于点![]() ,则
,则![]() _____.
_____.
【答案】(1)见解析;(2)①4;②![]()
【解析】
(1)连接OE.根据等腰三角形的性质得到∠OEB=∠C,根据平行线的性质得到∠OEF+∠AFE=180°.根据切线的判定定理即可得到结论;
(2)①连接BD,AE,根据圆周角定理得到∠ADB=90°,∠AEB=90°,求得AE⊥BC.根据勾股定理即可得到结论;
②根据勾股定理得到![]() ,CD=1,根据相似三角形的性质得到
,CD=1,根据相似三角形的性质得到![]() ,根据勾股定理即可得到结论.
,根据勾股定理即可得到结论.
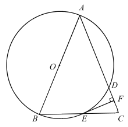
(1)连接![]() .
.
∵在![]() 中,
中,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() 于点
于点![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() .
.
∵![]() 于点
于点![]() ,
,![]() 是
是![]() 的半径,
的半径,
∴![]() 是
是![]() 的切线.
的切线.
(2)①连接![]() .
.
∵![]() 是
是![]() 的直径,
的直径,
∴![]() ,
,![]() .
.
∴![]() .
.
∵在![]() 中,
中,![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.
∴AB2-AD2=BC2-CD2.
设![]() ,则
,则![]() .
.
∴![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
②:∵AD=7,AB=AC=8,
∴![]() ,CD=1,
,CD=1,
∵BE=CE=2,EF∥BD,
∴![]() ,
,![]() ,
,
∵AB=AC,AE⊥BC,
∴∠BAE=∠CAE,
∴![]() ,
,
∴OE⊥BD,
∴OE⊥EF,
∴OE∥CF,
∴△CFM∽△OEM,
∴![]() ,
,
∴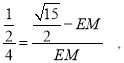
∴![]() ,
,
∴![]() .
.
故答案为:![]() .
.

 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案【题目】甲乙两人在相同条件下完成了10次射击训练,两人的成绩如图所示。

根据以上信息,整理分析数据如下:
平均成绩/环 | 中位数/环 | 方差/环 | |
甲 | ______ | 7 | 1.2 |
乙 | 7 | ______ | ______ |
(1)完成表格;
(2)根据训练成绩,你认为选派哪一名队员参赛更好?为什么?
【题目】受“新冠”疫情的影响,某销售商在网上销售![]() 、
、![]() 两种型号的“手写板”,获利颇丰.已知
两种型号的“手写板”,获利颇丰.已知![]() 型,
型,![]() 型手写板进价、售价和每日销量如表格所示:
型手写板进价、售价和每日销量如表格所示:
进价(元/个) | 售价(元/个) | 销量(个/日) | |
|
|
|
|
|
|
|
|
根据市场行情,该销售商对![]() 型手写板降价销售,同时对
型手写板降价销售,同时对![]() 型手写板提高售价,此时发现
型手写板提高售价,此时发现![]() 型手写板每降低
型手写板每降低![]() 元就可多卖
元就可多卖![]() 个,
个,![]() 型手写板每提高
型手写板每提高![]() 元就少卖
元就少卖![]() 个,要保持每天销售总量不变,设其中
个,要保持每天销售总量不变,设其中![]() 型手写板每天多销售
型手写板每天多销售![]() 个,每天总获利的利润为
个,每天总获利的利润为![]() 元
元
(1)求![]() 与
与![]() 之间的函数关系式并写出
之间的函数关系式并写出![]() 的取值范围;
的取值范围;
(2)要使每天的利润不低于![]() 元,直接写出
元,直接写出![]() 的取值范围;
的取值范围;
(3)该销售商决定每销售一个![]() 型手写板,就捐
型手写板,就捐![]() 元给
元给![]() 因“新冠疫情”影响的困难家庭,当
因“新冠疫情”影响的困难家庭,当![]() 时,每天的最大利润为
时,每天的最大利润为![]() 元,求
元,求![]() 的值.
的值.