题目内容
【题目】问题提出
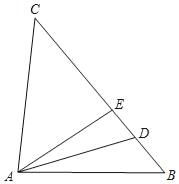
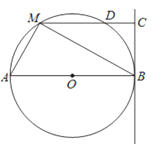
(1)如图①,在矩形ABCD中,AB=2AD,E为CD的中点,则∠AEB ∠ACB(填“>”“<”“=”);
问题探究
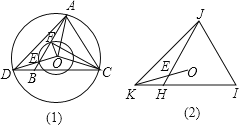
(2)如图②,在正方形ABCD中,P为CD边上的一个动点,当点P位于何处时,∠APB最大?并说明理由;
问题解决
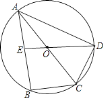
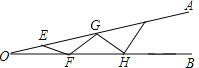
(3)如图③,在一幢大楼AD上装有一块矩形广告牌,其侧面上、下边沿相距6米(即AB=6米),下边沿到地面的距离BD=11.6米.如果小刚的睛睛距离地面的高度EF为1.6米,他从远处正对广告牌走近时,在P处看广告效果最好(视角最大),请你在图③中找到点P的位置,并计算此时小刚与大楼AD之间的距离.

【答案】(1)>;(2)当点P位于CD的中点时,∠APB最大,理由见解析;(3)4![]() 米.
米.
【解析】
(1)过点E作EF⊥AB于点F,由矩形的性质和等腰三角形的判定得到:△AEF是等腰直角三角形,易证∠AEB=90°,而∠ACB<90°,由此可以比较∠AEB与∠ACB的大小
(2)假设P为CD的中点,作△APB的外接圆⊙O,则此时CD切⊙O于P,在CD上取任意异于P点的点E,连接AE,与⊙O交于点F,连接BE、BF;由∠AFB是△EFB的外角,得∠AFB>∠AEB,且∠AFB与∠APB均为⊙O中弧AB所对的角,则∠AFB=∠APB,即可判断∠APB与∠AEB的大小关系,即可得点P位于何处时,∠APB最大;
(3)过点E作CE∥DF,交AD于点C,作AB的垂直平分线,垂足为点Q,并在垂直平分线上取点O,使OA=CQ,以点O为圆心,OB为半径作圆,则⊙O切CE于点G,连接OG,并延长交DF于点P,连接OA,再利用勾股定理以及长度关系即可得解.
解:(1)∠AEB>∠ACB,理由如下:
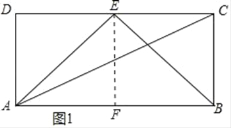
如图1,过点E作EF⊥AB于点F,
∵在矩形ABCD中,AB=2AD,E为CD中点,
∴四边形ADEF是正方形,
∴∠AEF=45°,
同理,∠BEF=45°,
∴∠AEB=90°.
而在直角△ABC中,∠ABC=90°,
∴∠ACB<90°,
∴∠AEB>∠ACB.
故答案为:>;
(2)当点P位于CD的中点时,∠APB最大,理由如下:
假设P为CD的中点,如图2,作△APB的外接圆⊙O,则此时CD切⊙O于点P,
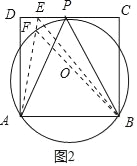
在CD上取任意异于P点的点E,连接AE,与⊙O交于点F,连接BE,BF,
∵∠AFB是△EFB的外角,
∴∠AFB>∠AEB,
∵∠AFB=∠APB,
∴∠APB>∠AEB,
故点P位于CD的中点时,∠APB最大:
(3)如图3,过点E作CE∥DF交AD于点C,作线段AB的垂直平分线,垂足为点Q,并在垂直平分线上取点O,使OA=CQ,
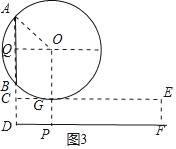
以点O为圆心,OA长为半径作圆,则⊙O切CE于点G,连接OG,并延长交DF于点P,此时点P即为小刚所站的位置,
由题意知DP=OQ=![]() ,
,
∵OA=CQ=BD+QB﹣CD=BD+![]() AB﹣CD,
AB﹣CD,
BD=11.6米,![]() AB=3米,CD=EF=1.6米,
AB=3米,CD=EF=1.6米,
∴OA=11.6+3﹣1.6=13米,
∴DP=![]() 米,
米,
即小刚与大楼AD之间的距离为4![]() 米时看广告牌效果最好.
米时看广告牌效果最好.

 阅读快车系列答案
阅读快车系列答案