题目内容
如图,在平面直角坐标系中,直线 与直线y=x交于点A,点B在直线
与直线y=x交于点A,点B在直线 上,∠BOA=90°.抛物线
上,∠BOA=90°.抛物线 过点A,O,B,顶点为点E.
过点A,O,B,顶点为点E.
(1)求点A,B的坐标;
(2)求抛物线的函数表达式及顶点E的坐标;
(3)设直线y=x与抛物线的对称轴交于点C,直线BC交抛物线于点D,过点E作FE∥x轴,交直线AB于点F,连接OD,CF,CF交x轴于点M.试判断OD与CF是否平行,并说明理由.
解:(1)由直线 与直线y=x交于点A,得
与直线y=x交于点A,得 ,解得,
,解得, 。
。
∴点A的坐标是(3,3)。
∵∠BOA=90°,∴OB⊥OA。
∴直线OB的解析式为y=﹣x。
又∵点B在直线 上,∴
上,∴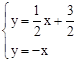 ,解得,
,解得,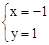 。
。
∴点B的坐标是(﹣1,1)。
综上所述,点A、B的坐标分别为(3,3),(﹣1,1)。
(2)由(1)知,点A、B的坐标分别为(3,3),(﹣1,1),
∵抛物线 过点A,O,B,
过点A,O,B,
∴ ,解得,
,解得,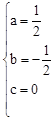 。
。
∴该抛物线的解析式为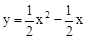 。
。
∵ ,∴顶点E的坐标是(
,∴顶点E的坐标是( ,
, )。
)。
(3)OD与CF平行。理由如下:
由(2)知,抛物线的对称轴是x= 。
。
∵直线y=x与抛物线的对称轴交于点C,∴C( ,
, )。
)。
设直线BC的表达式为 ,把B(﹣1,1),C(
,把B(﹣1,1),C( ,
, )代入,得
)代入,得 ,解得,
,解得, 。
。
∴直线BC的解析式为 。
。
∵直线BC与抛物线交于点B、D,∴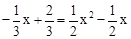 ,解得,x1=
,解得,x1=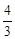 ,x2=﹣1.。
,x2=﹣1.。
把x1=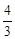 代入
代入 ,得y1=
,得y1=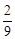 ,∴点D的坐标是(
,∴点D的坐标是(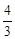 ,
,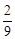 )。
)。
如图,作DN⊥x轴于点N,
则
∵FE∥x轴,点E的坐标为( ,
, ),
),
∴点F的纵坐标是 。
。
把y= 代入
代入 ,得x=
,得x= ,
,
∴点F的坐标是( ,
, ),
),
∴EF= 。
。
∵CE= ,∴
,∴ 。
。
∴∠CFE=∠DON。
又∵FE∥x轴,∴∠CMN=∠CFE。∴∠CMN=∠DON。
∴OD∥CF,即OD与CF平行。
解析试题分析:(1)由直线 与直线y=x交于点A,列出方程组
与直线y=x交于点A,列出方程组 ,通过解该方程组即可求得点A的坐标;根据∠BOA=90°得到直线OB的解析式为y=﹣x,则
,通过解该方程组即可求得点A的坐标;根据∠BOA=90°得到直线OB的解析式为y=﹣x,则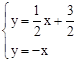 ,通过解该方程组来求点B的坐标即可。
,通过解该方程组来求点B的坐标即可。
(2)把点A、B、O的坐标分别代入已知二次函数解析式,列出关于系数a、b、c的方程组,通过解方程组即可求得该抛物线的解析式。
(3)如图,作DN⊥x轴于点N,欲证明OD与CF平行,只需证明同位角∠CMN与∠DON相等即可。

某商家独家销售具有地方特色的某种商品,每件进价为40元.经过市场调查,一周的销售量y件与销售单价x(x≥50)元/件的关系如下表:
| 销售单价x(元/件) | … | 55 | 60 | 70 | 75 | … |
| 一周的销售量y(件) | … | 450 | 400 | 300 | 250 | … |
(2)设一周的销售利润为S元,请求出S与x的函数关系式,并确定当销售单价在什么范围内变化时,一周的销售利润随着销售单价的增大而增大?
(3)雅安地震牵动亿万人民的心,商家决定将商品一周的销售利润全部寄往灾区,在商家购进该商品的贷款不超过10000元情况下,请你求出该商家最大捐款数额是多少元?
一汽车租赁公司拥有某种型号的汽车100辆.公司在经营中发现每辆车的月租金x(元)与每月租出的车辆数(y)有如下关系:
| x | 3000 | 3200 | 3500 | 4000 |
| y | 100 | 96 | 90 | 80 |
(2)已知租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.用含x(x≥3000)的代数式填表:
| 租出的车辆数 | | 未租出的车辆数 | |
| 租出每辆车的月收益 | | 所有未租出的车辆每月的维护费 | |
(2013年浙江义乌10分)为迎接中国森博会,某商家计划从厂家采购A,B两种产品共20件,产品的采购单价(元/件)是采购数量(件)的一次函数.下表提供了部分采购数据.
| 采购数量(件) | 1 | 2 | … |
| A产品单价(元/件) | 1480 | 1460 | … |
| B产品单价(元/件) | 1290 | 1280 | … |
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的
 ,且A产品采购单价不低于1200元.求该商家共有几种进货方案;
,且A产品采购单价不低于1200元.求该商家共有几种进货方案;(3)该商家分别以1760元/件和1700元/件的销售单价售出A,B两种产品,且全部售完.在(2)的条件下,求采购A种产品多少件时总利润最大,并求最大利润.




 与坐标轴分别交于点A、B,与直线y=x交于点C.在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形PEFQ总为矩形(点P、Q重合除外).
与坐标轴分别交于点A、B,与直线y=x交于点C.在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形PEFQ总为矩形(点P、Q重合除外).
 A,那么它的表达式可表示为:
A,那么它的表达式可表示为: ]
]