题目内容
一座桥如图,桥下水面宽度AB是20米,高CD是4米.要使高为3米的船通过,则其宽度须不超过多少米.
(1)如图1,若把桥看做是抛物线的一部分,建立如图坐标系.
①求抛物线的解析式;
②要使高为3米的船通过,则其宽度须不超过多少米?
(2)如图2,若把桥看做是圆的一部分.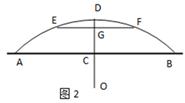
①求圆的半径;
②要使高为3米的船通过,则其宽度须不超过多少米?
(1)①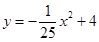 ;②10;(2)①14.5;②
;②10;(2)①14.5;②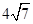 .
.
解析试题分析:(1)①利用待定系数法求函数解析式即可;②根据题意得出y=3时,求出x的值即可;
(2)①构造直角三角形利用BW2=BC2+CW2,求出即可;
②在RT△WGF中,由题可知,WF=14.5,WG=14.5﹣1=13.5,根据勾股定理知:GF2=WF2﹣WG2,求出即可.
试题解析:(1)①设抛物线解析式为: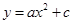 ,∵桥下水面宽度AB是20米,高CD是4米,∴A(﹣10,0),B(10,0),D(0,4),∴
,∵桥下水面宽度AB是20米,高CD是4米,∴A(﹣10,0),B(10,0),D(0,4),∴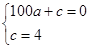 ,解得:
,解得: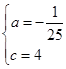 ,∴抛物线解析式为:
,∴抛物线解析式为: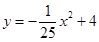 ;
;
②∵要使高为3米的船通过,∴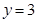 ,则
,则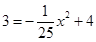 ,解得:
,解得: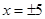 ,∴EF=10米;
,∴EF=10米;
(2)①设圆半径r米,圆心为W,∵BW2=BC2+CW2,∴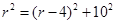 ,解得:
,解得: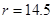 ;
;
②在RT△WGF中,由题可知,WF=14.5,WG=14.5﹣1=13.5,根据勾股定理知:GF2=WF2﹣WG2,即GF2=14.52﹣13.52=28,所以GF=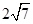 ,此时宽度EF=
,此时宽度EF=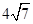 米.
米.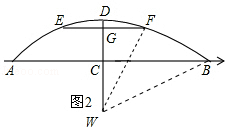
考点:1.二次函数的应用;2.垂径定理的应用.

练习册系列答案
相关题目
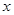 元(
元( 元.
元. 与y轴交于点(0,3).
与y轴交于点(0,3).
 )
) )
) .
. 的形式(要求写出配方过程);
的形式(要求写出配方过程); 与直线y=x交于点A,点B在直线
与直线y=x交于点A,点B在直线 过点A,O,B,顶点为点E.
过点A,O,B,顶点为点E.