题目内容
【题目】如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A( ![]() ,
, ![]() )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.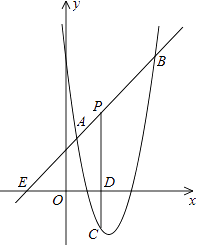
(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;
(3)求△PAC为直角三角形时点P的坐标.
【答案】
(1)
解:∵B(4,m)在直线y=x+2上,
∴m=4+2=6,
∴B(4,6),
∵A( ![]() ,
, ![]() )、B(4,6)在抛物线y=ax2+bx+6上,
)、B(4,6)在抛物线y=ax2+bx+6上,
∴ 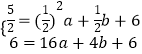 ,解得
,解得 ![]() ,
,
∴抛物线的解析式为y=2x2﹣8x+6
(2)
解:设动点P的坐标为(n,n+2),则C点的坐标为(n,2n2﹣8n+6),
∴PC=(n+2)﹣(2n2﹣8n+6),
=﹣2n2+9n﹣4,
=﹣2(n﹣ ![]() )2+
)2+ ![]() ,
,
∵PC>0,
∴当n= ![]() 时,线段PC最大且为
时,线段PC最大且为 ![]()
(3)
解:∵△PAC为直角三角形,
i)若点P为直角顶点,则∠APC=90°.
由题意易知,PC∥y轴,∠APC=45°,因此这种情形不存在;
ii)若点A为直角顶点,则∠PAC=90°.
如答图3﹣1,过点A( ![]() ,
, ![]() )作AN⊥x轴于点N,则ON=
)作AN⊥x轴于点N,则ON= ![]() ,AN=
,AN= ![]() .
.
过点A作AM⊥直线AB,交x轴于点M,则由题意易知,△AMN为等腰直角三角形,
∴MN=AN= ![]() ,∴OM=ON+MN=
,∴OM=ON+MN= ![]() +
+ ![]() =3,
=3,
∴M(3,0).
设直线AM的解析式为:y=kx+b,
则: 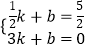 ,解得
,解得 ![]() ,
,
∴直线AM的解析式为:y=﹣x+3 ①
又抛物线的解析式为:y=2x2﹣8x+6 ②
联立①②式,解得:x=3或x= ![]() (与点A重合,舍去)
(与点A重合,舍去)
∴C(3,0),即点C、M点重合.
当x=3时,y=x+2=5,
∴P1(3,5);
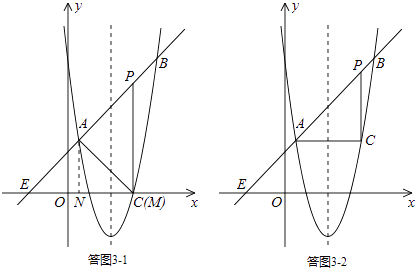
iii)若点C为直角顶点,则∠ACP=90°.
∵y=2x2﹣8x+6=2(x﹣2)2﹣2,
∴抛物线的对称轴为直线x=2.
如答图3﹣2,作点A( ![]() ,
, ![]() )关于对称轴x=2的对称点C,
)关于对称轴x=2的对称点C,
则点C在抛物线上,且C( ![]() ,
, ![]() ).
).
当x= ![]() 时,y=x+2=
时,y=x+2= ![]() .
.
∴P2( ![]() ,
, ![]() ).
).
∵点P1(3,5)、P2( ![]() ,
, ![]() )均在线段AB上,
)均在线段AB上,
∴综上所述,△PAC为直角三角形时,点P的坐标为(3,5)或( ![]() ,
, ![]() )
)
【解析】(1)已知B(4,m)在直线y=x+2上,可求得m的值,抛物线图象上的A、B两点坐标,可将其代入抛物线的解析式中,通过联立方程组即可求得待定系数的值.(2)要弄清PC的长,实际是直线AB与抛物线函数值的差.可设出P点横坐标,根据直线AB和抛物线的解析式表示出P、C的纵坐标,进而得到关于PC与P点横坐标的函数关系式,根据函数的性质即可求出PC的最大值.(3)当△PAC为直角三角形时,根据直角顶点的不同,有三种情形,需要分类讨论,分别求解.
【考点精析】根据题目的已知条件,利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

 同步拓展阅读系列答案
同步拓展阅读系列答案