题目内容
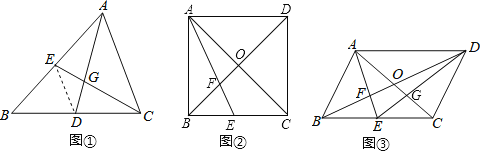
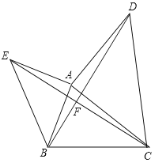
【题目】如图,已知△ABC,分别以AB,AC为直角边,向外作等腰直角三角形ABE和等腰直角三角形ACD,∠EAB=∠DAC=90°,连结BD,CE交于点F,设AB=m,BC=n.下列结论①∠BDA=∠ECA; ②若m=![]() ,n=3,∠ABC=75°,则BD=
,n=3,∠ABC=75°,则BD=![]() ;③当∠ABC=135°时,BD最大,最大值为
;③当∠ABC=135°时,BD最大,最大值为![]() m+n;④AE2=BF2+EF2中正确的有_______。
m+n;④AE2=BF2+EF2中正确的有_______。
【答案】①②③
【解析】
(1)利用△ABE和△ACD是等腰直角三角形,可得△BAD≌△EAC(SAS),进而得出∠BDA=∠ACE;
(2)作EG⊥CB,交CB的延长线与G点,先求得∠EBG=60°,再根据勾股定理即可得到BD的长;
(3)当B,E,C三点共线时,EC取最大值,∠ABC=135°.依据EC=BE+BC=![]() m+n,可得BD=
m+n,可得BD=![]() m+n;
m+n;
(4)依据全等三角形的性质可得∠AEF=∠ABF,进而得出∠EFB=90°,依据勾股定理可得EB2=BF2+EF2,依据BE=![]() AE,即可得出2AE2=BF2+EF2.
AE,即可得出2AE2=BF2+EF2.
①∵△ABE和△ACD是等腰直角三角形,
∴AE=AB,AC=AD,∠BAE=∠CAD=90°,∠ACD=∠ADC=45°,
∴∠BAE+∠BAC=∠CAD+∠BAC,
∴∠CAE=∠BAD,
在△BAD和△EAC中,
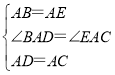 ,
,
∴△BAD≌△EAC(SAS),
∴∠BDA=∠ACE,
故①正确;
②如图,作EG⊥CB,交CB的延长线与G点,
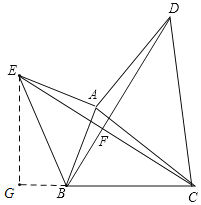
∵等腰直角三角形ABE,AE=AB=![]() ,
,
∴∠ABE=45°,BE=2,
∵∠ABC=75°,
∴∠EBG=60°,
∴BG=1,
∴根据勾股定理得EG=![]()
∵BC=3,
∴CG=4,
∴根据勾股定理可得,EC2=EG2+CG2,
解得CE=![]() ,
,
∴根据(1)得BD=CE=![]() ,
,
故②正确;
③在△EBC中,BE=![]() m,BC=n,
m,BC=n,
根据三角形三边关系可得BE+BC>EC,
∴当B,E,C三点共线时,EC取最大值,∠ABC=135°.如图所示:
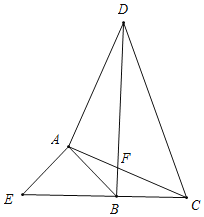
∴EC=BE+BC=![]() m+n,
m+n,
即BD=![]() m+n,
m+n,
故③正确;
④∵△EAC≌△BAD,
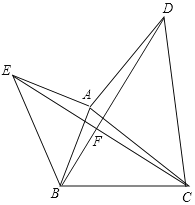
∴∠AEF=∠ABF,
∵∠AEB+∠ABE=90°,
∴∠EFB=90°,
∴EB2=BF2+EF2,
∵BE=![]() AE,
AE,
∴2AE2=BF2+EF2.
故④错误.
故答案为:①②③.

 阅读快车系列答案
阅读快车系列答案