题目内容
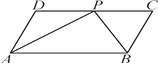
【题目】如图,平行四边形ABCD的边OA在x轴上,将平行四边形沿对角线AC对折,AO的对应线段为AD,且点D,C,O在同一条直线上,AD与BC交于点E.

(1)求证:△ABC≌△CDA.
(2)若直线AB的函数表达式为![]() ,求三角线ACE的面积.
,求三角线ACE的面积.
【答案】(1)证明见详解;(2)![]()
【解析】
(1)利用平行四边形的性质及折叠的性质,可得出CD=AB,∠DCA=∠BAC,结合AC=CA可证出△ABC≌△CDA(SAS);
(2)由点D,C,O在同一直线上可得出∠DCA=∠OCA=90°,利用一次函数图象上点的坐标特征可得出点A的坐标及OA的长度,由OC∥AB可得出直线OC的解析式为y=x,进而可得出∠COA=45°,结合∠OCA=90°可得出△AOC为等腰直角三角形,利用等腰直角三角形的性质可得出OC、AC的长,结合(1)的结论可得出四边形ABDC为正方形,再利用正方形的面积公式结合S△ACE=![]() S正方形ABDC可求出△ACE的面积.
S正方形ABDC可求出△ACE的面积.
(1)证明:∵四边形ABCO为平行四边形,
∴AB=CO,AB∥OC,
∴∠BAC=∠OCA.
由折叠可知:CD=CO,∠DCA=∠OCA,
∴CD=AB,∠DCA=∠BAC.
在△ABC和△CDA中,
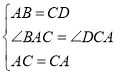 ,
,
∴△ABC≌△CDA(SAS).
(2)解:∵∠DCA=∠OCA,点D,C,O在同一直线上,
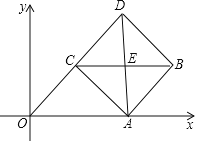
∴∠DCA=∠OCA=90°.
当y=0时,x-6=0,解得:x=6,
∴点A的坐标为(6,0),OA=6.
∵OC∥AB,
∴直线OC的解析式为y=x,
∴∠COA=45°,
∴△AOC为等腰直角三角形,
∴AC=OC=![]() .
.
∵AB∥CD,AB=CD=AC,∠DCA=90°,
∴四边形ABDC为正方形,
![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案【题目】足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度![]() (单位:
(单位:![]() )与足球被踢出后经过的时间
)与足球被踢出后经过的时间![]() (单位:
(单位:![]() )之间的关系如下表:
)之间的关系如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
下列结论:①足球距离地面的最大高度为![]() ;②足球飞行路线的对称轴是直线
;②足球飞行路线的对称轴是直线![]() ;③足球被踢出
;③足球被踢出![]() 时落地;④足球被踢出
时落地;④足球被踢出![]() 时,距离地面的高度是
时,距离地面的高度是![]() .
.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
【题目】树叶有关的问题
如图,一片树叶的长是指沿叶脉方向量出的最长部分的长度(不含叶柄),树叶的宽是指沿与主叶脉垂直方向量出的最宽处的长度,树叶的长宽比是指树叶的长与树叶的宽的比值。

某同学在校园内随机收集了A树、B树、C树三棵的树叶各10片,通过测量得到这些树叶的长y(单位:cm),宽x(单位:cm)的数据,计算长宽比,理如下:
表1 A树、B树、C树树叶的长宽比统计表
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
A树树叶的长宽比 | 4.0 | 4.9 | 5.2 | 4.1 | 5.7 | 8.5 | 7.9 | 6.3 | 7.7 | 7.9 |
B树树叶的长宽比 | 2.5 | 2.4 | 2.2 | 2.3 | 2.0 | 1.9 | 2.3 | 2.0 | 1.9 | 2.0 |
C树树叶的长宽比 | 1.1 | 1.2 | 1.2 | 0.9 | 1.0 | 1.0 | 1.1 | 0.9 | 1.0 | 1.3 |
表1 A树、B树、C树树叶的长宽比的平均数、中位数、众数、方差统计表
平均数 | 中位数 | 众数 | 方差 | |
A树树叶的长宽比 | 6.2 | 6.0 | 7.9 | 2.5 |
B树树叶的长宽比 | 2.2 | 0.38 | ||
C树树叶的长宽比 | 1.1 | 1.1 | 1.0 | 0.02 |
A树、B树、C树树叶的长随变化的情况

解决下列问题:
(1)将表2补充完整;
(2)①小张同学说:“根据以上信息,我能判断C树树叶的长、宽近似相等。”
②小李同学说:“从树叶的长宽比的平均数来看,我认为,下图的树叶是B树的树叶。”
![]()
请你判断上面两位同学的说法中,谁的说法是合理的,谁的说法是不合理的,并给出你的理由;
(3)现有一片长103cm,宽52cm的树叶,请将该树叶的数用“★”表示在图1中,判断这片树叶更可能来自于A、B、C中的哪棵树?并给出你的理由。
【题目】某商场用14500元购进甲、乙两种矿泉水共500箱,矿泉水的成本价与销售价如表(二)所示:
类别 | 成本价(元/箱) | 销售价(元/箱) |
甲 | 25 | 35 |
乙 | 35 | 48 |
求:(1)购进甲、乙两种矿泉水各多少箱?
(2)该商场售完这500箱矿泉水,可获利多少元?