ĢāÄæÄŚČŻ
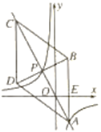
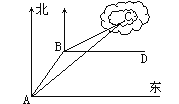
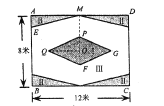
”¾ĢāÄæ”æČēĶ¼1£¬ŌŚĆ껿ĪŖ49cm2µÄµČŃüRt”÷ABCÖ½°åÖŠ£¬ŌŚÖ±½Ē±ßAB£¬ACÉĻø÷Č”Ņ»µćE£¬F£¬BE£½CF£¬DĪŖBCµÄÖŠµć£¬½«”÷BDE£¬”÷CDF·Ö±šŃŲDE£¬DFÕŪµž£¬¶ŌÓ¦±ßB”äD£¬C”äD·Ö±š½»AB£¬ACÓŚµćG£¬H£¬ŌŁ½«”÷AGHŃŲGHÕŪĮ棬µćAµÄ¶ŌÓ¦µćAĀäŌŚ”÷GHDµÄÄŚ²æ£ØČēĶ¼2ĖłŹ¾£©£¬·Ćę»ÉĻŃŪ¾¦ŗĶ±Ē×Ó£¬µĆµ½ĮĖŅ»·łæÉ°®µÄ”°ĆØĮ³Ķ¼”±£ØČēĶ¼3ĖłŹ¾£©£¬ČōµćB”äÓėµćC”äÖ®¼äµÄ¾ąĄėĪŖ![]() cm£¬ŌņĪå±ßŠĪGHFDEµÄĆ껿ĪŖ_____cm2£®
cm£¬ŌņĪå±ßŠĪGHFDEµÄĆ껿ĪŖ_____cm2£®
”¾“š°ø”æ![]()
”¾½āĪö”æ
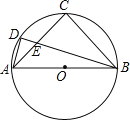
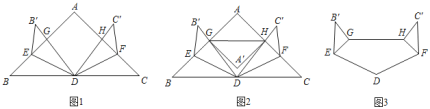
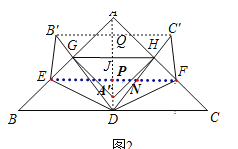
Į¬½ÓAD£¬B”äC”䣬EF£¬AD½»GHÓŚJ£¬½»B”äC”äÓŚQ£¬½»EFÓŚP£¬EF½»C”äDÓŚN£®ŌŚRt”÷DHB”äÖŠ£¬ĄūÓĆ¹“¹É¶ØĄķĒó³öDQ£¬tan”ĻQDC”䣽![]() £½
£½![]() £½
£½![]() £¬ÉčJH£½3a£¬JD£½4a£¬ŌņAJ£½JH£½3a£¬¹¹½Ø·½³ĢĒó³öa£¬ÉčPN=3b£¬PD=4b£¬Ķ¬ĄķæÉĒóµĆb=
£¬ÉčJH£½3a£¬JD£½4a£¬ŌņAJ£½JH£½3a£¬¹¹½Ø·½³ĢĒó³öa£¬ÉčPN=3b£¬PD=4b£¬Ķ¬ĄķæÉĒóµĆb=![]() £¬¼“æɽā¾öĪŹĢā£®
£¬¼“æɽā¾öĪŹĢā£®
½ā£ŗČēĶ¼£¬Į¬½ÓAD£¬B”äC”䣬EF£¬AD½»GHÓŚJ£¬½»B”äC”äÓŚQ£¬½»EFÓŚP£¬EF½»C”äDÓŚN£®ŌņÓÉÕŪµžµÄŠŌÖŹÖŖBC//EF//GH// B”äC”䣮
”ßAB£½AC£¬”ĻBAC£½90”ć£¬BD£½DC£¬
”ąAD”ĶBC£¬AD£½BD£½CD£¬
”ßS”÷ABC£½![]() BCAD£½AD2£½49£¬
BCAD£½AD2£½49£¬
”ąAD£½BD£½CD£½7£¬
ÓÉĢāŅā£ŗB”äQ£½C”äQ£½![]() £¬
£¬
ŌŚRt”÷DQB”äÖŠ£¬DQ£½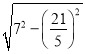 £½
£½![]() £¬
£¬
”ątan”ĻQDC”䣽![]() £½
£½![]() £½
£½![]() £¬ÉčJH£½3a£¬JD£½4a£¬ŌņAJ£½JH£½3a£¬
£¬ÉčJH£½3a£¬JD£½4a£¬ŌņAJ£½JH£½3a£¬
”ą7a£½7£¬
”ąa£½1£¬
”ąJH£½AJ£½3£¬DJ£½4£¬
ÉčPN=3b£¬PD=4b£¬ŌņND=5b£®
”ßBC//EF£¬
”ą”ĻPND=”ĻNDC£¬
”ß”ĻPND=”ĻNDF+”ĻNFD£¬”ĻNDC=”ĻNDF+”ĻFDC£¬”ĻNDF=”ĻFDC£¬
”ą”ĻNDF=NFD£¬
”ąNF=ND=5b£¬
”ąPF=3b+5b=8b£®
”ß”ĻAFP=”ĻC=45”ć£¬
”ąAP=PF=5b£¬
”ąAD=8b+4b=12b£¬
”ą12b=7£¬
”ąb=![]() £¬
£¬
”ąPD=![]() £®
£®
”ąSĪå±ßŠĪ
£½49©![]() ”Į6”Į3©2”Į
”Į6”Į3©2”Į![]() ”Į7”Į
”Į7”Į![]()
£½![]() £¬
£¬
¹Ź“š°øĪŖ![]() £®
£®

”¾ĢāÄæ”æijČÕĶõĄĻŹ¦Åå“÷ŌĖ¶ÆŹÖ»·½ųŠŠæģ×߶ĶĮ¶Į½“Ī¶ĶĮ¶ŗóŹż¾ŻČēĻĀ±ķ£¬ÓėµŚŅ»“Ī¶ĶĮ¶Ļą±Č£¬ĶõĄĻŹ¦µŚ¶ž“Ī¶ĶĮ¶²½ŹżŌö³¤µÄ°Ł·ÖĀŹŹĒĘäĘ½¾ł²½³¤¼õÉŁµÄ°Ł·ÖĀŹµÄ![]() ±¶.ÉčĶõĄĻŹ¦µŚ¶ž“Ī¶ĶĮ¶Ź±Ę½¾ł²½³¤¼õÉŁµÄ°Ł·ÖĀŹĪŖ
±¶.ÉčĶõĄĻŹ¦µŚ¶ž“Ī¶ĶĮ¶Ź±Ę½¾ł²½³¤¼õÉŁµÄ°Ł·ÖĀŹĪŖ![]() £®×¢£ŗ²½Źż
£®×¢£ŗ²½Źż![]() Ę½¾ł²½³¤
Ę½¾ł²½³¤![]() ¾ąĄė£®
¾ąĄė£®
ĻīÄæ | µŚŅ»“Ī¶ĶĮ¶ | µŚ¶ž“Ī¶ĶĮ¶ |
²½Źż£Ø²½£© |
| ¢Ł_______ |
Ę½¾ł²½³¤£ØĆ×/²½£© |
| ¢Ś_______ |
¾ąĄė£ØĆ×£© |
|
|
£Ø1£©øł¾ŻĢāŅāĶź³É±ķøń£»
£Ø2£©Ēó![]() £®
£®
”¾ĢāÄæ”æČēĶ¼£¬Ä³Š£×¼±øøų³¤12Ć×£¬æķ8Ć׵ľŲŠĪ![]() ŹŅÄŚ³”µŲ½ųŠŠµŲĆę×°ŹĪ£¬ĻÖ½«Ęä»®·ÖĪŖĒųÓņ¢ń£ØĮāŠĪ
ŹŅÄŚ³”µŲ½ųŠŠµŲĆę×°ŹĪ£¬ĻÖ½«Ęä»®·ÖĪŖĒųÓņ¢ń£ØĮāŠĪ![]() £©£¬ĒųÓņ¢ņ£Ø4øöČ«µČµÄÖ±½ĒČż½ĒŠĪ£©£¬Ź£Óąæհײæ·Ö¼ĒĪŖĒųÓņ¢ó£»µć
£©£¬ĒųÓņ¢ņ£Ø4øöČ«µČµÄÖ±½ĒČż½ĒŠĪ£©£¬Ź£Óąæհײæ·Ö¼ĒĪŖĒųÓņ¢ó£»µć![]() ĪŖ¾ŲŠĪŗĶĮāŠĪµÄ¶Ō³ĘÖŠŠÄ£¬
ĪŖ¾ŲŠĪŗĶĮāŠĪµÄ¶Ō³ĘÖŠŠÄ£¬![]() £¬
£¬![]() £¬
£¬![]() £¬ĪŖĮĖĆĄ¹Ū£¬ŅŖĒóĒųÓņ¢ņµÄĆ껿²»³¬¹ż¾ŲŠĪ
£¬ĪŖĮĖĆĄ¹Ū£¬ŅŖĒóĒųÓņ¢ņµÄĆ껿²»³¬¹ż¾ŲŠĪ![]() Ć껿µÄ
Ć껿µÄ![]() £¬ČōÉč
£¬ČōÉč![]() Ć×.
Ć×.
¼× | ŅŅ | ±ū | |
µ„¼Ū£ØŌŖ/Ć×2£© |
|
|
|
£Ø1£©µ±![]() Ź±£¬ĒóĒųÓņ¢ņµÄĆ껿.
Ź±£¬ĒóĒųÓņ¢ņµÄĆ껿.
£Ø2£©¼Ę»®ŌŚĒųÓņ¢ń£¬¢ņ·Ö±šĘĢÉč¼×£¬ŅŅĮ½æī²»Ķ¬µÄÉīÉ«“Éש£¬ĒųÓņ¢óĘĢÉč±ūæī°×É«“Éש£¬
¢ŁŌŚĻąĶ¬¹āÕÕĢõ¼žĻĀ£¬µ±³”µŲÄŚ°×É«ĒųÓņµÄĆ껿Ō½“ó£¬ŹŅÄŚ¹āĻßĮĮ¶ČŌ½ŗĆ.µ±![]() ĪŖ¶ąÉŁŹ±£¬ŹŅÄŚ¹āĻßĮĮ¶Č×īŗĆ£¬²¢Ēó“ĖŹ±°×É«ĒųÓņµÄĆ껿.
ĪŖ¶ąÉŁŹ±£¬ŹŅÄŚ¹āĻßĮĮ¶Č×īŗĆ£¬²¢Ēó“ĖŹ±°×É«ĒųÓņµÄĆ껿.
¢ŚČżÖÖ“ÉשµÄµ„¼ŪĮŠ±ķČēĻĀ£¬![]() ¾łĪŖÕżÕūŹż£¬Čōµ±
¾łĪŖÕżÕūŹż£¬Čōµ±![]() Ć׏±£¬¹ŗĀņČżæī“ÉשµÄ×Ü·ŃÓĆ×īÉŁ£¬ĒŅ×īÉŁ·ŃÓĆĪŖ7200ŌŖ£¬“ĖŹ±
Ć׏±£¬¹ŗĀņČżæī“ÉשµÄ×Ü·ŃÓĆ×īÉŁ£¬ĒŅ×īÉŁ·ŃÓĆĪŖ7200ŌŖ£¬“ĖŹ±![]() __________£¬
__________£¬