Question

【题目】在中，的垂直平分线交于点，交于点.

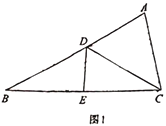
（1）如图1，若，，，求的长；

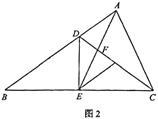
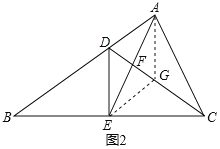
（2）如图2，连接交于点，若为的中点，且满足，求证：.

Answer 1

【答案】（1）；（2）证明见解析．

【解析】

（1）作AF⊥CD于F，由线段垂直平分线的性质得出BD=CD，由等腰三角形的性质得出∠DCB=∠B=30°，∠BAC=∠BCA=75°，求出∠ACF=45°，得出△ACF是等腰直角三角形，得出AF=1，∠FAC=45°，由直角三角形的性质得出DF的长，即可得出答案；

（2）作AG∥DE交CD于G，则∠GAF=∠DEF，证明△AFG≌△EFD(ASA)，得出AG=ED，GF=DF，证出四边形ADEG是平行四边形，得出AD=EG，∠DAG+∠ADE=180°，证明△ADE≌△CGA(SAS)，得出∠DAE=∠GCA，进而得出结论．

（1）作AF⊥CD于F，如图1所示：

∵DE是BC的垂直平分线，

∴BD=CD，

∴∠DCB=∠B=30°．

∵BA=BC，

∴∠BAC=∠BCA(180°﹣30°)=75°，

∴∠ACF=75°﹣30°=45°．

∵AF⊥CD，

∴△ACF是等腰直角三角形，

∴AF=CFAC=1，∠FAC=45°，

∴∠DAF=30°，

∴DFAF，

∴BD=CD=CF+DF=；

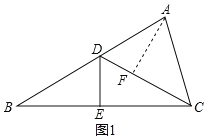
（2）作AG∥DE交CD于G，如图2所示：

则∠GAF=∠DEF．

∵F为AE的中点，

∴AF=EF．

在△AFG和△EFD中，

∵，

∴△AFG≌△EFD(ASA)，

∴AG=ED，GF=DF．

∵AG∥ED，

∴四边形ADEG是平行四边形，

∴AD=EG，∠DAG+∠ADE=180°．

∵DA+2DF=DB=DC，DC=DF+GF+CG，

∴AD=CG=EG，

∴∠GEC=∠GCE．

∵∠GEC+∠DEG=∠GCE+∠GDE=90°，

∴∠DEG=∠GDE，

∴DG=EG=CG=AD，

∴∠DAG=∠DGA．

∵∠DGA+∠CGA=180°，

∴∠ADE=∠CGA．

在△ADE和△CGA中，

∵，

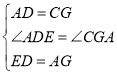∴△ADE≌△CGA(SAS)，

∴∠DAE=∠GCA．

∵∠DAC=∠DAE+∠CAF，∠EFC=∠GCA+∠CAF，

∴∠DAC=∠EFC．