题目内容
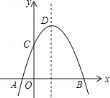
【题目】如图,直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
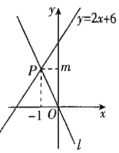
(1)求m的值;
(2)方程组![]() 的解是________;
的解是________;
(3)直线![]() 是否也经过点P?请判断并说明理由.
是否也经过点P?请判断并说明理由.
【答案】(1)m=4;(2) ![]() ;(3)经过,理由见解析
;(3)经过,理由见解析
【解析】
(1)把点![]() 的坐标代入直线
的坐标代入直线![]() 得到一个关于m的一元一次方程,解这个方程即可;
得到一个关于m的一元一次方程,解这个方程即可;
(2)由(1)可求得点![]() 的坐标,由图象可知直线l经过原点,所以b=0,再把点
的坐标,由图象可知直线l经过原点,所以b=0,再把点![]()
的坐标代入即可求出k的值,再让这两条直线解析式联立组成二元一次方程组求解即可;
(3)根据点P的坐标为![]() ,在直线
,在直线![]() 上,可得出
上,可得出![]() ,然后再将
,然后再将![]() 代人直线
代人直线![]() 中,得
中,得![]() ,从而得出结论.
,从而得出结论.
(1)将点![]() 代入直线
代入直线![]() ,得
,得![]() ,解得
,解得![]() .
.
(2)由(1)可知点![]() 坐标为(-1,4),依题意得:
坐标为(-1,4),依题意得:
![]() 解得:
解得:![]()
∴直线![]() 的解析式为
的解析式为![]()
联立两个直线解析式得:![]()
解得:![]() .
.
故答案为![]() .
.
(3)直线![]() 也经过点P.理由如下
也经过点P.理由如下
![]() 点P的坐标为
点P的坐标为![]() ,在直线
,在直线![]() 上,
上,
![]() .
.
将![]() 代人直线
代人直线![]() 中,得
中,得![]() ,
,
![]() 直线
直线![]() 也经过点.
也经过点.

【题目】如图,在菱形ABCD中,AE⊥BC于E,将△ABE沿AE所在直线翻折得△AEF,若AB=2,∠B=45°,则△AEF与菱形ABCD重叠部分(阴影部分)的面积为( ).
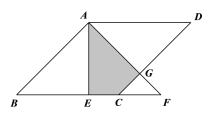
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
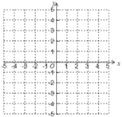
【题目】已知抛物线![]()
抛物线 | 顶点坐标 | 与x轴交点坐标 | 与y轴交点坐标 | |
抛物线 | A(____) | B(____) | (1,0) | (0,-3) |
(1)补全表中A,B两点的坐标,并在所给的平面直角坐标系中,画出抛物线![]()
(2)结合图象回答
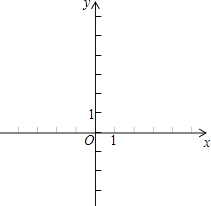
①当x的取值范围为________时,y随x的增大而增大;
②当x________时,![]() ;
;
③当![]() 时,y的取值范围________.
时,y的取值范围________.
【题目】甲、乙两名同学分别进行6次射击训练,训练成绩(单位:环)如下表
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六交 | |
甲 | 9 | 8 | 6 | 7 | 8 | 10 |
乙 | 8 | 7 | 9 | 7 | 8 | 8 |
对他们的训练成绩作如下分析,其中说法正确的是( )
A. 他们训练成绩的平均数相同 B. 他们训练成绩的中位数不同
C. 他们训练成绩的众数不同 D. 他们训练成绩的方差不同