题目内容
【题目】如图,AB是半圆O的直径,AB=a,C是半圆上一点,弦AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,连接CD,DB,OD. 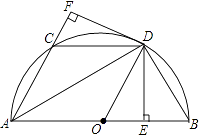
(1)求证:△CDF≌△BDE;
(2)当AD=时,四边形AODC是菱形;
(3)当AD=时,四边形AEDF是正方形.
【答案】
(1)证明:∵弦AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,
∴DE=DF.
∵弦AD平分∠BAC,
∴∠FAD=∠BAD,
∴BD=CD.
在Rt△BED和Rt△CFD中 ![]() ,
,
∴Rt△BED≌Rt△CFD (HL);
(2)![]()
(3)![]() a
a
【解析】解:(2)四边形AODC是菱形时, OD=CD=DB=OB,
∴∠DBA=60°,
∴AD=ABcos∠DBA=asin60°= ![]() a,
a,
故答案为: ![]() ;(3)当OD⊥AB,即OD与OE重合时,四边形AEDF是正方形,
;(3)当OD⊥AB,即OD与OE重合时,四边形AEDF是正方形,
由勾股定理,得
AD= ![]() =
= ![]() a,
a,
故答案为: ![]() a.
a.
(1)根据角平分线的性质,可得DF与DE的关系,根据圆周角定理,可得DC与DB的关系,根据HL,可得答案;(2)根据菱形的性质,可得OD与CD,OD与BD的关系,根据正三角形的性质,可得∠DBA的度数,根据三角函数值,可得答案;(3)根据圆周角定理,可得OD⊥AB,根据勾股定理,可得答案.

练习册系列答案
相关题目
【题目】某校八年级一班20名女生某次体育测试的成绩统计如下:
成绩(分) | 60 | 70 | 80 | 90 | 100 |
人数(人) | 1 | 5 | x | y | 2 |
(1)如果这20名女生体育成绩的平均分数是82分,求x、y的值;
(2)在(1)的条件下,设20名学生测试成绩的众数是a,中位数是b,求![]() 的值.
的值.