题目内容
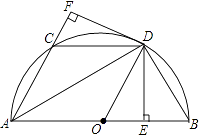
【题目】如图，隧道的截面由抛物线和长方形构成，长方形的长是12m，宽是4m．按照图中所示的直角坐标系，抛物线可以用y=﹣ 
x2+bx+c表示，且抛物线的点C到墙面OB的水平距离为3m时，到地面OA的距离为 
m． 
（1）求该抛物线的函数关系式，并计算出拱顶D到地面OA的距离；
（2）一辆货运汽车载一长方体集装箱后高为6m，宽为4m，如果隧道内设双向行车道，那么这辆货车能否安全通过？
（3）在抛物线型拱壁上需要安装两排灯，使它们离地面的高度相等，如果灯离地面的高度不超过8m，那么两排灯的水平距离最小是多少米？
【答案】
（1）解：根据题意得B（0，4），C（3， 
），
把B（0，4），C（3， ）代入y=﹣ 
x2+bx+c得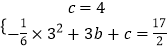 
，
解得 
．
所以抛物线解析式为y=﹣ x2+2x+4，
则y=﹣ （x﹣6）2+10，
所以D（6，10），
所以拱顶D到地面OA的距离为10m；
（2）解：由题意得货运汽车最外侧与地面OA的交点为（2，0）或（10，0），
当x=2或x=10时，y= 
＞6，
所以这辆货车能安全通过；
（3）解：令y=8，则﹣ （x﹣6）2+10=8，解得x1=6+2 
，x2=6﹣2 ，
则x1﹣x2=4 ，
所以两排灯的水平距离最小是4 m．
【解析】（1）先确定B点和C点坐标，然后利用待定系数法求出抛物线解析式，再利用配方法确定顶点D的坐标，从而得到点D到地面OA的距离；（2）由于抛物线的对称轴为直线x=6，而隧道内设双向行车道，车宽为4m，则货运汽车最外侧与地面OA的交点为（2，0）或（10，0），然后计算自变量为2或10的函数值，再把函数值与6进行大小比较即可判断；（3）抛物线开口向下，函数值越大，对称点之间的距离越小，于是计算函数值为8所对应的自变量的值即可得到两排灯的水平距离最小值．
