题目内容
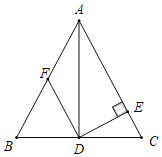
【题目】如图,Rt△ABC 有一外接圆,其中∠B=90°,AB>BC,今欲在![]() 上找一点 P, 使得
上找一点 P, 使得![]() ,下是甲、乙两人的作法:
,下是甲、乙两人的作法:
甲:①取 AB 的中点 D:②过点 D 作直线 AC 的平行线,交![]() 于点 P,则点 P 即为所求,
于点 P,则点 P 即为所求,
乙:①取 AC 的中点 E;②过点 E 作直线AB 的平行线,交![]() 于点 P,则点 P 即为所求,
于点 P,则点 P 即为所求,
对于甲、乙两人的作法,下列判断正确的是( )
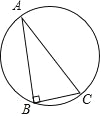
A. 两人皆正确 B. 两人皆错误 C. 甲正确,乙错误 D. 甲错误,乙正确
【答案】B
【解析】
(1)由甲的作法可知,DP是△ABC的中位线,由于DP不垂直于BC,故![]() ≠
≠![]() ;
;
(2)由乙的作法,连BE,可知△BEC为等腰三角形,由等腰三角形的性质可知∠1=∠2,根据圆周角定理即可得出结论.
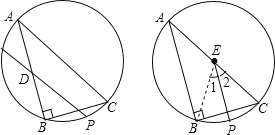
(1)由甲的作法可知,DP是△ABC的中位线,
∵DP不垂直于BC,∴![]() ≠
≠![]() ;
;
(2)由乙的作法,连BE,可知△BEC为等腰三角形
∵直线PE⊥BC,∴∠1=∠2
故![]() =
=![]() ;∴甲错误,乙正确.故选B.
;∴甲错误,乙正确.故选B.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
【题目】某批发商以每件50元的价格购进400件T恤.若以单价70元销售,预计可售出200件.批发商的销售策略是:第一个月为增加销售量,降价销售,经过市场调查,单价每降低0.5元,可多售出5件,但最低单价不低于购进的价格;第一个月结束后,将剩余的T恤一次性清仓销售,清仓时单价为40元.设第一个月单价降低x元.
(1)根据题意,完成下表:
每件T恤的利润(元) | 销售量(件) | |
第一个月 | ||
清仓时 |
(2)T恤的销售单价定为多少元时,该批发商可获得最大利润?最大利润为多少?