ĖâÄŋÄÚČÝ
ĄūĖâÄŋĄŋķĻŌåĢš
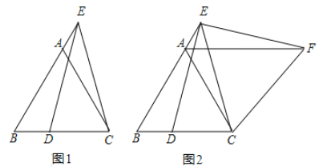
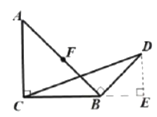
ĘýŅ§ŧîķŊŋÎÉÏĢŽĀîĀÏĘĶļøģöČįÏÂķĻŌåĢšČįđûŌŧļöČý―ĮÐÎÓÐŌŧąßÉÏĩÄÖÐÏßĩČÓÚÕâĖõąßĩÄŌŧ°ëĢŽÄĮÃīģÆÕâļöČý―ĮÐÎΊĄ°ÖĮŧÛČý―ĮÐÎĄąĢŪ
Āí―âĢš
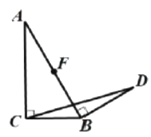
ĢĻ1ĢĐČįÍžĢŽŌŅÖŠ![]() ĄĒ
ĄĒ![]() ĘĮ
ĘĮ![]() ÉÏÁ―ĩãĢŽĮëÔÚÔēÉÏÕŌģöÂúŨãĖõžþĩÄĩã
ÉÏÁ―ĩãĢŽĮëÔÚÔēÉÏÕŌģöÂúŨãĖõžþĩÄĩã![]() ĢŽĘđ
ĢŽĘđ![]() ΊĄ°ÖĮŧÛČý―ĮÐÎĄąĢĻŧģöĩã
ΊĄ°ÖĮŧÛČý―ĮÐÎĄąĢĻŧģöĩã![]() ĩÄÎŧÖÃĢŽąĢÁôŨũÍžšÛžĢĢĐĢŧ
ĩÄÎŧÖÃĢŽąĢÁôŨũÍžšÛžĢĢĐĢŧ
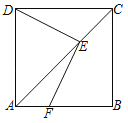
ĢĻ2ĢĐČįÍžĢŽÔÚÕý·―ÐÎ![]() ÖÐĢŽ
ÖÐĢŽ![]() ĘĮ
ĘĮ![]() ĩÄÖÐĩãĢŽ
ĩÄÖÐĩãĢŽ![]() ĘĮ
ĘĮ![]() ÉÏŌŧĩãĢŽĮŌ
ÉÏŌŧĩãĢŽĮŌ![]() ĢŽĘÔÅÐķÏ
ĢŽĘÔÅÐķÏ![]() ĘĮ·ņΊĄ°ÖĮŧÛČý―ĮÐÎĄąĢŽēĒËĩÃũĀíÓÉĢŧ
ĘĮ·ņΊĄ°ÖĮŧÛČý―ĮÐÎĄąĢŽēĒËĩÃũĀíÓÉĢŧ
ÔËÓÃĢš
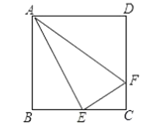
ĢĻ3ĢĐČįÍžĢŽÔÚÆ―ÃæÖą―ĮŨøąęÏĩ![]() ÖÐĢŽ
ÖÐĢŽ![]() ĩÄ°ëūķΊ1ĢŽĩã
ĩÄ°ëūķΊ1ĢŽĩã![]() ĘĮÖąÏß
ĘĮÖąÏß![]() ÉÏĩÄŌŧĩãĢŽČôÔÚ
ÉÏĩÄŌŧĩãĢŽČôÔÚ![]() ÉÏīæÔÚŌŧĩã
ÉÏīæÔÚŌŧĩã![]() ĢŽĘđĩÃ
ĢŽĘđĩÃ![]() ΊĄ°ÖĮŧÛČý―ĮÐÎĄąĢŽĩąÆäÃæŧýČĄĩÃŨîÐĄÖĩĘąĢŽÖą―ÓÐīģöīËĘąĩã
ΊĄ°ÖĮŧÛČý―ĮÐÎĄąĢŽĩąÆäÃæŧýČĄĩÃŨîÐĄÖĩĘąĢŽÖą―ÓÐīģöīËĘąĩã![]() ĩÄŨøąęĢŪ
ĩÄŨøąęĢŪ
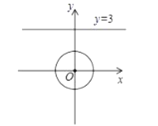
Ąūīð°ļĄŋĢĻ1ĢĐžû―âÎöĢŧĢĻ2ĢĐ![]() ĘĮ·ņΊĄ°ÖĮŧÛČý―ĮÐÎĄąĢŽĀíÓÉžû―âÎöĢŧĢĻ3ĢĐĩã
ĘĮ·ņΊĄ°ÖĮŧÛČý―ĮÐÎĄąĢŽĀíÓÉžû―âÎöĢŧĢĻ3ĢĐĩã![]() ĩÄŨøąę
ĩÄŨøąę ĢŽ
ĢŽ ĢŪ
ĢŪ
Ąū―âÎöĄŋ
ĢĻ1ĢĐÁŽ―áAOēĒĮŌŅÓģĪ―ŧÔēÓÚC1ĢŽÁŽ―áBOēĒĮŌŅÓģĪ―ŧÔēÓÚC2ĢŽžīŋÉĮó―âĢŧ
ĢĻ2ĢĐÉčÕý·―ÐÎĩÄąßģĪΊ4aĢŽąíĘūģöDFĄĒCFŌÔž°ECĄĒBEĩÄģĪĢŽČŧšóļųūÝđīđÉķĻĀíÁÐĘ―ąíĘūģöAF2ĄĒEF2ĄĒAE2ĢŽÔŲļųūÝđīđÉķĻĀíÄæķĻĀíÅÐķĻĄũAEFĘĮÖą―ĮČý―ĮÐÎĢŽÓÉÖą―ĮČý―ĮÐÎĩÄÐÔÖĘŋÉĩÃĄũAEFΊĄ°ÖĮŧÛČý―ĮÐÎĄąĢŧ
ĢĻ3ĢĐļųūÝĄ°ÖĮŧÛČý―ĮÐÎĄąĩÄķĻŌåŋÉĩÃĄũOPQΊֹ―ĮČý―ĮÐÎĢŽļųūÝĖâŌâŋÉĩÃŌŧĖõÖą―ĮąßΊ1ĢŽĩąÐąąßŨîķĖĘąĢŽÁíŌŧĖõÖą―ĮąßŨîķĖĢŽÔōÃæŧýČĄĩÃŨîÐĄÖĩĢŽÓÉīđÏßķÎŨîķĖŋÉĩÃÐąąßŨîķĖΊ3ĢŽļųūÝđīđÉķĻĀíŋÉĮóÁíŌŧĖõÖą―ĮąßĢŽÔŲļųūÝČý―ĮÐÎÃæŧýŋÉĮóÐąąßĩÄļßĢŽžīĩãPĩÄšáŨøąęĢŽÔŲļųūÝđīđÉķĻĀíŋÉĮóĩãPĩÄŨÝŨøąęĢŽīÓķøĮó―âĢŪ
ĢĻ1ĢĐ―âÎöĄŋČįÍžËųĘū

ĢĻ2ĢĐ![]() ĘĮ·ņΊĄ°ÖĮŧÛČý―ĮÐÎĄąĢŽ
ĘĮ·ņΊĄ°ÖĮŧÛČý―ĮÐÎĄąĢŽ
ĀíÓÉČįÏÂĢšÉčÕý·―ÐÎĩÄąßģĪΊ![]() ĢŽ
ĢŽ
Ąß![]() ĘĮ
ĘĮ![]() ĩÄÖÐĩãĢŽĄā
ĩÄÖÐĩãĢŽĄā![]() ĢŽ
ĢŽ
Ąß![]() ĢŽĄā
ĢŽĄā![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ
ÔÚ![]() ÖÐĢŽ
ÖÐĢŽ![]() ĢŽ
ĢŽ
ÔÚ![]() ÖÐĢŽ
ÖÐĢŽ![]() ĢŽ
ĢŽ
ÔÚ![]() ÖÐĢŽ
ÖÐĢŽ![]() ĢŽ
ĢŽ
Ąā![]() ĢŽ
ĢŽ
Ąā![]() ĘĮÖą―ĮČý―ĮÐÎĢŽ
ĘĮÖą―ĮČý―ĮÐÎĢŽ
ĄßÐąąß![]() ÉÏĩÄÖÐÏßĩČÓÚ
ÉÏĩÄÖÐÏßĩČÓÚ![]() ĩÄŌŧ°ëĢŽ
ĩÄŌŧ°ëĢŽ
Ąā![]() ΊĄ°ÖĮŧÛČý―ĮÐÎĄąĢŧ
ΊĄ°ÖĮŧÛČý―ĮÐÎĄąĢŧ
ĢĻ3ĢĐČįÍžËųĘūĢš

ÓÉĄ°ÖĮŧÛČý―ĮÐÎĄąĩÄķĻŌåŋÉĩÃ![]() Ίֹ―ĮČý―ĮÐÎĢŽ
Ίֹ―ĮČý―ĮÐÎĢŽ
ļųūÝĖâŌâŋÉĩÃŌŧĖõÖą―ĮąßΊ1ĢŽĩąÐąąßŨîķĖĘąĢŽÁíŌŧĖõÖą―ĮąßŨîķĖĢŽÔōÃæŧýČĄĩÃŨîÐĄÖĩĢŽÓÉīđÏßķÎŨîķĖŋÉĩÃÐąąßŨîķĖΊ3ĢŽ
ÓÉđīđÉķĻĀíŋÉĩÃ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ
ÓÉđīđÉķĻĀíŋÉĮóĩÃ ĢŽ
ĢŽ
đĘĩã![]() ĩÄŨøąę
ĩÄŨøąę ĢŽ
ĢŽ ĢŪ
ĢŪ