题目内容
【题目】如图1,在圆O中,直径CD⊥弦AB于点E,点P是CD延长线上一点,连接PB、BD.
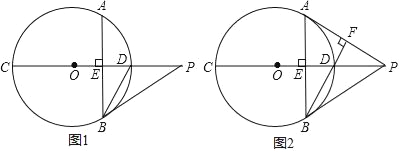
(1)若BD平分∠ABP,求证:PB是圆O的切线;
(2)若PB是圆O的切线,AB=4,OP=4,求OE的长;
(3)如图2,连接AP,延长BD交AP于点F,若BD⊥AP,AB=2![]() ,OP=4,求tan∠BDE的值.
,OP=4,求tan∠BDE的值.
【答案】(1)见解析;(2)OE=2;(3)tan∠BDE=![]() .
.
【解析】
(1)连接BC,BO,根据圆周角定理得到∠CBD=90°,根据等腰三角形的性质得到∠OBC=∠C,于是得到结论;
(2)设OB=r,OE=x,证△OBE∽△OPB得![]() ,即r2=4x,在Rt△OBE中,由OB2=OE2+BE2可得关于x的方程,解之可得答案;
,即r2=4x,在Rt△OBE中,由OB2=OE2+BE2可得关于x的方程,解之可得答案;
(3)连接BC,BO,根据已知条件得到AP∥BC,根据平行线的性质得到∠C=∠APC,根据垂径定理得到AE=BE,根据等腰三角形的性质得到CE=PE,设OE=x,CO=BO=r,根据勾股定理即可得到x的值,进一步可得DE的长,根据三角函数的定义可得答案.
解:(1)连接BC,BO,
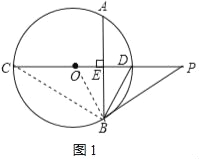
∵CD是⊙O的直径,
∴∠CBD=90°,
∵CD⊥AB,
∴∠DBE=∠C=90°﹣∠CDB,
∵OB=OC,
∴∠OBC=∠C,
∵∠PBD=∠EBD,
∴∠PBD=∠OBC,
∴∠PBO=90°,
∴PB是⊙O的切线;
(2)设OB=r,OE=x,
∵PB为⊙O的切线,CD⊥AB,
∴∠OBP=∠OEB=90°,
又∵∠BOE=∠POB,
∴△OBE∽△OPB,
则![]() ,即
,即![]() ,
,
∴r2=4x,
∵AB=4,CD⊥AB,
∴AE=BE=2,
在Rt△OBE中,由OB2=OE2+BE2可得4x=x2+4,
解得:x=2,即OE=2;
(3)如图2,连接BC,BO,

∵CD是⊙O的直径,
∴BC⊥BD,
∵BD⊥AP,
∴AP∥BC,
∴∠C=∠APC,
∵CD是⊙O的直径,CD⊥AB,
∴AE=BE,
∴AP=BP,
∴∠APC=∠BPC,
∴∠C=∠BPC,
∴CE=PE,
设OE=x,CO=BO=r,
∴r+x=4﹣x,
∴r=4﹣2x,
∵AB=2![]() ,
,
∴BE=![]() AB=
AB=![]() ,
,
在Rt△BEO中,BO2=OE2+BE2,即(4﹣2x)2=x2+(![]() )2,
)2,
解得:x=1或x=![]() (不合题意,舍去),
(不合题意,舍去),
∴OE=1、OD=OB=4﹣2=2,
则DE=OD﹣OE=1,
∴tan∠BDE=![]() =
=![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案