题目内容
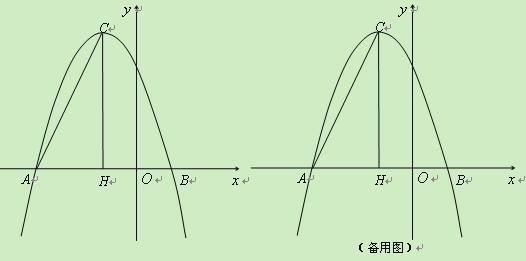
【题目】如图，抛物线y＝ax2+bx+c交x轴于A、B 两点，交 y 轴于 C点，其中﹣2＜h＜﹣1，﹣1＜xB＜0，下列结论：①abc＞0；②4a﹣2b+c＞0；③5a+2c＞3b；④（4a﹣b）（2a+b）＜0；正确的有（ ）个．
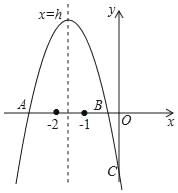
A. 4 B. 3 C. 2 D. 1
【答案】B
【解析】
①由抛物线对称轴位置确定ab的符号，由抛物线与y轴的交点判断c与0的关系，进而对所得结论进行判断；
②当x＝﹣2时，y＞0，代入得4a﹣2b+c＞0，可作判断；
③根据b＞4a，得2b﹣8a＞0①，当x＝﹣1，x＝﹣2时，y＞0，则有a﹣b+c＞0①，4a﹣2b+c＞0②，两式相加可得结论；
④根据对称轴公式和﹣2＜h＜﹣1可得：4a﹣b＜0，根据a＜0，b＜0可知：2a+b＜0，可作判断．
①∵抛物线开口向下，
抛物线对称轴位于y轴的左侧，则a、b同号，故ab＞0，
抛物线与y轴交于负半轴，则c＜0，故abc＜0，
故①正确；
②抛物线y＝ax2+bx+c交x轴于A、B 两点，其中﹣2＜h＜﹣1，﹣1＜xB＜0，
∴当x＝﹣2时，y＞0，即4a﹣2b+c＞0，
故②正确；
③∵当x＝﹣1时，y＞0，即a﹣b+c＞0①，当x＝﹣2时，y＞0，即4a﹣2b+c＞0，4a﹣2b+c＞0②，
∴①+②得，5a﹣3b+2c＞0，即5a+2c＞3b，
故③正确；
④∵抛物线开口方向向下，
∴a＜0，
∵x＝﹣
＝h，且﹣2＜h＜﹣1，
∴4a＜b＜2a，
∴4a﹣b＜0，
又∵h＜0，
∴﹣＜1
∴2a+b＜0，
∴（4a﹣b）（2a+b）＞0，
故④错误；
所以本题正确的有：①②③，
故选：B．
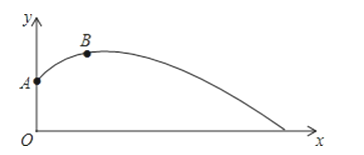
期末宝典单元检测分类复习卷系列答案
【题目】小明为了检测自己实心球的训练情况，再一次投掷的测试中，实心球经过的抛物线如图所示，其中出手点A的坐标为（0，
），球在最高点B的坐标为（3，
）．
（1）求抛物线的解析式；
（2）已知某市男子实心球的得分标准如表：
得分 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
掷远（米） | 8.6 | 8.3 | 8 | 7.7 | 7.3 | 6.9 | 6.5 | 6.1 | 5.8 | 5.5 | 5.2 | 4.8 | 4.4 | 4.0 | 3.5 | 3.0 |
假设小明是春谷中学九年级的男生，求小明在实心球训练中的得分；
（3）在小明练习实心球的正前方距离投掷点7米处有一个身高1.2米的小朋友在玩耍，问该小朋友是否有危险（如果实心球在小孩头顶上方飞出为安全，否则视为危险），请说明理由．
