ЬтФПФкШн
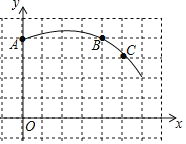
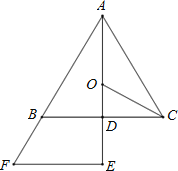
ЁОЬтФПЁПШчЭМЃЌдкСтаЮABCDжаЃЌ![]() ЁЂ
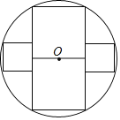
ЁЂ![]() ЁЂ
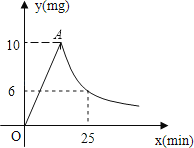
ЁЂ![]() ЗжБ№ЪЧСтаЮABCDЕФСНЬѕЖдНЧЯпГЄКЭБпГЄЃЌетЪБЮвУЧАбЙигк
ЗжБ№ЪЧСтаЮABCDЕФСНЬѕЖдНЧЯпГЄКЭБпГЄЃЌетЪБЮвУЧАбЙигк![]() ЕФаЮШчЁА
ЕФаЮШчЁА![]() ЁБЕФвЛдЊЖўДЮЗНГЬГЦЮЊЁАСтЯЕвЛдЊЖўДЮЗНГЬЁБЃЎЧыНтОіЯТСаЮЪЬтЃК
ЁБЕФвЛдЊЖўДЮЗНГЬГЦЮЊЁАСтЯЕвЛдЊЖўДЮЗНГЬЁБЃЎЧыНтОіЯТСаЮЪЬтЃК

ЃЈ1ЃЉЬюПеЃКЂйЕБ![]() ЃЌ
ЃЌ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЎ
ЃЎ
ЂкгУКЌ![]() ЃЌ
ЃЌ![]() ЕФДњЪ§ЪНБэЪО
ЕФДњЪ§ЪНБэЪО![]() жЕЃЌ
жЕЃЌ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉЧѓжЄЃКЙигк![]() ЕФЁАСтЯЕвЛдЊЖўДЮЗНГЬЁБ
ЕФЁАСтЯЕвЛдЊЖўДЮЗНГЬЁБ![]() БигаЪЕЪ§ИљЃЛ
БигаЪЕЪ§ИљЃЛ
ЃЈ3ЃЉШє![]() ЪЧЁАСтЯЕвЛдЊЖўДЮЗНГЬЁБ
ЪЧЁАСтЯЕвЛдЊЖўДЮЗНГЬЁБ![]() ЕФвЛИіИљЃЌЧвСтаЮЕФУцЛ§ЪЧ25ЃЌBEЪЧСтаЮABCDЕФADБпЩЯЕФИпЃЌЧѓBEЕФжЕЃЎ
ЕФвЛИіИљЃЌЧвСтаЮЕФУцЛ§ЪЧ25ЃЌBEЪЧСтаЮABCDЕФADБпЩЯЕФИпЃЌЧѓBEЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂй5ЃЌЂк![]() ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉ
ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉНсКЯЭМаЮЃЌИљОнСтаЮЕФЖдНЧЯпЛЅЯрЦНЗжвдМАЙДЙЩЖЈРэМДПЩЕУЕННсТлЃЛ
ЃЈ2ЃЉЫуГіЁїЃЌНсКЯЃЈ1ЃЉжаЂкЕФНсТлМДПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉИљОнЗНГЬИљЕФЖЈвхЕУГіmЁЂnЁЂtЕФЙиЯЕЃЌНсКЯЃЈ1ЃЉжаЂкЕФНсТлНјааЛЏМђЃЌдйИљОнСтаЮУцЛ§ЪЧ25ЃЌМДПЩЕУГіtЕФжЕЃЌНјЖјЕУГіНсТлЃЎ
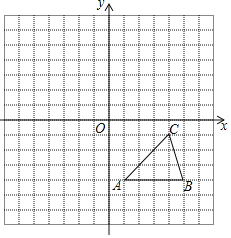
ЃЈ1ЃЉЂйЕБm=6ЃЌn=8ЪБЃЌAO=4ЃЌOB=3ЃЌЁрt=AB=![]() =5ЃЎ
=5ЃЎ
ЂкЁпAO=![]() ЃЌOB=
ЃЌOB=![]() ЃЌЁрt2=AB2=
ЃЌЁрt2=AB2=![]() ЃЎ
ЃЎ
ЙЪД№АИЮЊЃК5ЃЌ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉ![]()
етРяЃЌa=mЃЌb=![]() tЃЌc=nЃЌЁр
tЃЌc=nЃЌЁр![]() ЃЎ
ЃЎ
Ёп![]() ЃЌЁр
ЃЌЁр![]()
![]() ЃЌЁрЙигк
ЃЌЁрЙигк![]() ЕФЁАСтЯЕвЛдЊЖўДЮЗНГЬЁБ
ЕФЁАСтЯЕвЛдЊЖўДЮЗНГЬЁБ![]() БигаЪЕЪ§ИљЃЎ
БигаЪЕЪ§ИљЃЎ
ЃЈ3ЃЉЁп![]() ЪЧЁАСтЯЕвЛдЊЖўДЮЗНГЬЁБ
ЪЧЁАСтЯЕвЛдЊЖўДЮЗНГЬЁБ![]() ЕФвЛИіИљЃЌЁр
ЕФвЛИіИљЃЌЁр![]() ЃЌЁр
ЃЌЁр![]() ЃЌЁр
ЃЌЁр![]() ЃЎ
ЃЎ
Ёп![]() ЃЌЁр
ЃЌЁр![]() ЃЎ
ЃЎ
ЁпСтаЮУцЛ§ЪЧ25ЃЌЁр![]() ЃЌЁр
ЃЌЁр![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌМД
ЃЌМД![]() ЃЌЁр
ЃЌЁр![]() ЃЎ
ЃЎ