Question

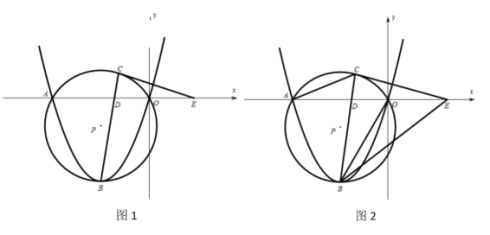
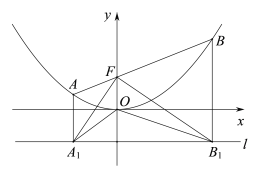
【题目】如图，抛物线（p＞0），点F（0，p），直线l：y=-p，已知抛物线上的点到点F的距离与到直线l的距离相等，过点F的直线与抛物线交于A，B两点，AA1⊥l，BB1⊥l，垂足分别为A1、B1，连接A1F，B1F，A1O，B1O．若A1F=a，B1F=b、则△A1OB1的面积=____．（只用a，b表示）．

Answer 1

【答案】.

【解析】

根据题意可知SA1OB1=SA1B1F,=，从而得到本题的结果.

解：∵AA1⊥l，y轴⊥l，

∴AA1∥y轴.

∴∠AA1F=∠A1FO.

∵AF=AA1,

∴∠AA1F=∠A1FA.

∴∠A1FO=∠A1FA.

同理可证：∠B1FO=∠B1FB.

∴∠A1FB1=90°.

∴△A1FB1的面积=A1FB1F=.

∵抛物线上的点到点F的距离与到直线l的距离相等，

∴O到到点F的距离与到直线l的距离相等，

∴△A1OB1的面积=△A1FB1的面积=.