题目内容
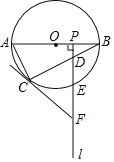
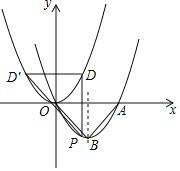
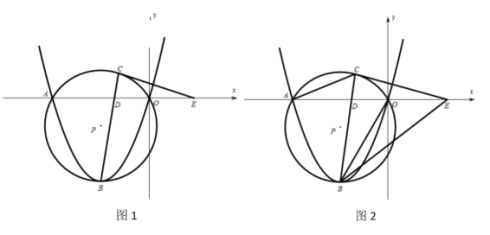
【题目】如图，抛物线
(a为常数，a＞0)与x轴交于O，A两点，点B为抛物线的顶点，点D的坐标为(t，0)(﹣3＜t＜0)，连接BD并延长与过O，A，B三点的⊙P相交于点C．
（1）求点A的坐标；
（2）过点C作⊙P的切线CE交x轴于点E．①如图1，求证：CE＝DE；②如图2，连接AC，BE，BO，当
，∠CAE＝∠OBE时，求
的值
【答案】（1）A（－6,0）；（2）①见解析 ；②
【解析】
（1）令y=0，可得ax（x+6）=0，则A点坐标可求出；
（2）①连接PC，连接PB延长交x轴于点M，由切线的性质可证得∠ECD=∠COE，则CE=DE；
②设OE=m，由CE2=OEAE，可得m＝
，由∠CAE=∠OBE可得
，则m＝
，综合整理代入
可求出
的值．
（1）令ax2+bax=0
ax（x+6）=0
∴A（－6,0）
（2）连接PC，连接PB延长交x轴于M
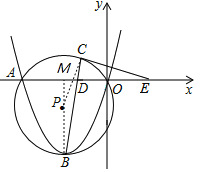
过O、A、B三点，B为顶点
，
又∵PC=PB
，
∵CE为切线
°，
又
，
∴CE=DE，
（3）设OE=m，即E（m,0）
由切割定理：CE2=OE·AE
，
，
已知
，
由角平分线定理：
即：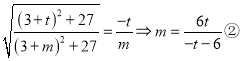
由①②得
∴t2=－18t－36
，
练习册系列答案
阅读快车系列答案
相关题目
