题目内容
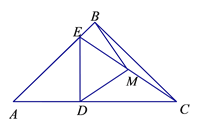
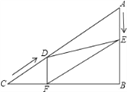
【题目】如图1,已知点A(﹣2,0),点B(0,﹣4),AD与y轴交于点E,且E为AD的中点,双曲线y=![]() 经过C,D两点且D(a,8)、C(4,b).
经过C,D两点且D(a,8)、C(4,b).
(1)求a、b、k的值;
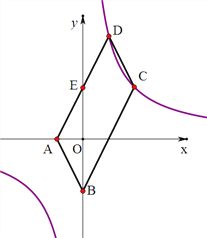
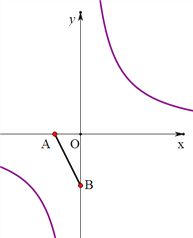
(2)如图2,点P在双曲线y=![]() 上,点Q在x轴上,若以A、B、P、Q为顶点的四边形为平行四边形,试直接写出满足要求的所有点Q的坐标.
上,点Q在x轴上,若以A、B、P、Q为顶点的四边形为平行四边形,试直接写出满足要求的所有点Q的坐标.
【答案】(1) a=2,k=16,b=4;(2) Q1(6,0)或Q1(-6,0)Q1(2,0).
【解析】分析:
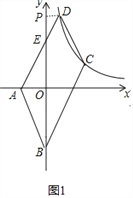
(1)如下图,过点D作DP⊥y轴于点P,结合已知条件可证得△PDE≌△OAE,由此可得PD==a=OA=2,这样即可得到点D的坐标,将点D的坐标代入![]() 中即可求得k的值,再结合点C(4,b)在该反比例函数的图象上即可求得b的值;
中即可求得k的值,再结合点C(4,b)在该反比例函数的图象上即可求得b的值;
(2)如下图,分AB为所求平行四边形的边和对角线两种情况结合已知条件分析讨论即可.
(1)如图1,过点D作DP⊥y轴于点P,
∵点E为AD的中点,
∴AE=DE.
又∵DP⊥y轴,∠AOE=90°,
∴∠DPE=∠AEO.
∵在△PDE与△OAE中,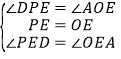 ,
,
∴△PDE≌△OAE(ASA),
∴PD=OA,
∵A(﹣2,0),
∴a=2,
∴D(2,8).
∵点D在反比例函数图象上,
∴k=xy=2×8=16.
∵点C在反比例函数图象上,C的坐标为(4,b),
∴b=![]() =4,
=4,
∴a=2,k=16,b=4;
(2)∵点P在双曲线![]() 上,点Q在x轴上,
上,点Q在x轴上,
∴可设点P的坐标为![]() ,点Q的坐标为(m,0),
,点Q的坐标为(m,0),
如下图,①当AB为所求平行四边形ABP1Q1的边时,由点B的坐标为(0,-4)可得点P此时的坐标(-4,-4),∴PB=AQ1=4,
∴OQ1=OA+AQ1=6,
∴此时点Q1的坐标为(-6,0);
②当AB为所求平行四边形ABQ2P2的边时,由平行四边形的性质可知点P到x轴的距离=点B到x轴的距离=4,
∴点P此时的坐标为(4,4);
又∵点P可以可知是由点A平移得到的,而点Q2可以看着是由点B平移得到的,
∴由平移的性质可得点Q2的坐标为(6,0);
③当AB为所求平行四边形AP1BQ3的对角线时,由AQ3=PB结合①中所得PB=4可得AQ3=4,
∵AO=2,
∴OQ3=4-2=2,
∴Q3的坐标为(2,0);
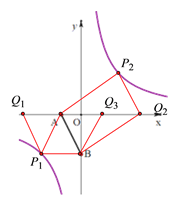
综上所述,满足条件的点Q有3个,坐标分别为:Q1(-6,0)或Q2(6,0)或Q3(2,0).

【题目】自行车厂某周计划生产2100辆电动车,平均每天生产电动车300辆.由于各种原因,实际每天的生产量与计划每天的生产量相比有出入,下表是该周的实际生产情况(超产记为正、减产记为负,单位:辆):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
减增 |
|
|
|
|
|
|
|
(1)该厂星期一生产电动车________辆;
(2)生产量最多的一天比生产量最少的一天多生产电动车________辆;
(3)该厂实行记件工资制,每生产一辆车可得60元,那么该厂工人这一周的工资总额是多少元?