题目内容
【题目】已知:在Rt△ABC中,AB=BC;在Rt△ADE中,AD=DE;连结EC,取EC的中点M,连结DM和BM.
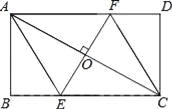
(1)若点D在边AC上,点E在边AB上且与点B不重合,如图①,
求证:BM=DM且BM⊥DM;
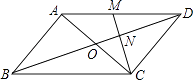
(2)如果将图①中的△ADE绕点A逆时针旋转小于45°的角,如图②,那么(1)中的结论是否仍成立?如果不成立,请举出反例;如果成立,请给予证明.
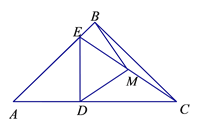

图① 图②
【答案】(1)证明见解析(2)当△ADE绕点A逆时针旋转小于45°的角时,(1)中的结论成立
【解析】分析:(1)、根据直角三角形斜边上的中线的性质得出BM=DM,然后根据四点共圆可以得出∠BMD=2∠ACB=90°,从而得出答案;(2)、连结BD,延长DM至点F,使得DM=MF,连结BF、FC,延长ED交AC于点H,根据题意得出四边形CDEF为平行四边形,然后根据题意得出△ABD和△CBF全等,根据角度之间的关系得出∠DBF=∠ABC =90°.
详解:(1)在Rt△EBC中,M是斜边EC的中点,∴![]() .
.
在Rt△EDC中,M是斜边EC的中点,∴![]() .
.
∴BM=DM,且点B、C、D、E在以点M为圆心、BM为半径的圆上.
∴∠BMD=2∠ACB=90°,即BM⊥DM.
(2)当△ADE绕点A逆时针旋转小于45°的角时,(1)中的结论成立.
证明:连结BD,延长DM至点F,使得DM=MF,连结BF、FC,延长ED交AC于点H.
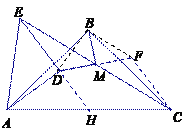
∵ DM=MF,EM=MC, ∴ 四边形CDEF为平行四边形,∴ DE∥CF ,ED =CF,
∵ ED= AD,∴ AD=CF, ∵ DE∥CF,∴ ∠AHE=∠ACF.
∵![]() ,
,![]() ,
,
∴ ∠BAD=∠BCF, 又∵AB= BC, ∴ △ABD≌△CBF,∴ BD=BF,∠ABD=∠CBF,
∵ ∠ABD+∠DBC =∠CBF+∠DBC,∴∠DBF=∠ABC =90°.
在Rt△![]() 中,由
中,由![]() ,
, ![]() ,得BM=DM且BM⊥DM.
,得BM=DM且BM⊥DM.

 星级口算天天练系列答案
星级口算天天练系列答案