题目内容
已知关于x的方程x2-(k+2)x+2k=0,若一个等腰三角形的一边长为1,另两边长恰是这个方程的两个根,求这个等腰三角形的周长与面积.
分析:首先根据题意利用因式分解法求得x2-(k+2)x+2k=0的解,又由一个等腰三角形的一边长为1,利用分类讨论思想,根据三角形的三边关系,即可求得k的值,继而求得这个等腰三角形的周长与面积.
解答:解:∵x2-(k+2)x+2k=0,
∴(x-k)(x-2)=0,
解得:x1=2,x2=k,
∵三角形是等腰三角形,
当k=1时,不能围成三角形;
当k=2时,周长为5;
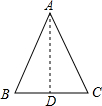 如图:设AB=AC=2,BC=1,
如图:设AB=AC=2,BC=1,
过点A作AD⊥BC于D,
∴BD=CD=
BC=
,
∴AD=
=
,
∴S△ABC=
×1×
=
.
故面积为
.
∴(x-k)(x-2)=0,
解得:x1=2,x2=k,
∵三角形是等腰三角形,
当k=1时,不能围成三角形;
当k=2时,周长为5;
 如图:设AB=AC=2,BC=1,
如图:设AB=AC=2,BC=1,过点A作AD⊥BC于D,
∴BD=CD=
| 1 |
| 2 |
| 1 |
| 2 |
∴AD=
| AB2-BD2 |
| ||
| 2 |
∴S△ABC=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
故面积为
| ||
| 4 |
点评:此题考查了因式分解法解一元二次方程、等腰三角形的性质以及三角形的三边关系.此题难度适中,注意掌握分类讨论思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目