题目内容
【题目】如图，
为锐角三角形，
是
边上的高，正方形
的一边
在上，顶点
、
分别在
、
上．已知
，
．
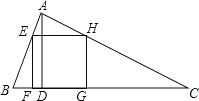
（1）求证：
；
（2）求这个正方形的面积．
【答案】（1）见详解；（2）
【解析】
（1）根据EH∥BC即可证明．
（2）如图设AD与EH交于点M，首先证明四边形EFDM是矩形，设正方形边长为x，再利用△AEH∽△ABC，得
，列出方程即可解决问题．
（1）证明：∵四边形EFGH是正方形，
∴EH∥BC，
∴∠AEH＝∠B，∠AHE＝∠C，
∴△AEH∽△ABC．
（2）解：如图设AD与EH交于点M．
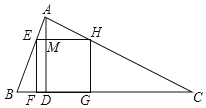
∵∠EFD＝∠FEM＝∠FDM＝90°，
∴四边形EFDM是矩形，
∴EF＝DM，设正方形EFGH的边长为x，
∵△AEH∽△ABC，
∴，
∴
，
∴x＝
，
∴x2＝，
∴正方形EFGH的面积为cm2．
练习册系列答案
相关题目
【题目】商贸公司购进某种水果的成本为20元/kg，经过市场调研发现，这种水果在未来48天的销售单价p（元/kg）与时间t（天）之间的函数关系式为p=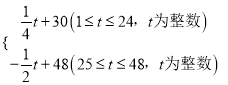
，且其日销售量y（kg）与时间t（天）的关系如表：
时间t（天） | 1 | 3 | 6 | 10 | 20 | 40 | … |
日销售量y（kg） | 118 | 114 | 108 | 100 | 80 | 40 | … |
（1）已知y与t之间的变化规律符合一次函数关系，试求在第30天的日销售量是多少？
（2）问哪一天的销售利润最大？最大日销售利润为多少？