Question

【题目】如图，是规格为8×8的正方形网格，请在所给网格中按下列要求操作：

(1)在网格中建立平面直角坐标系，使A点坐标为(-2，4)，B点坐标为(-4，2)；

(2)在(1)的前提下，在第二象限内的格点上找一点C，使点C与线段AB组成一个以AB为底的等腰三角形，且腰长是无理数，则C点的坐标是；

(3)求((2)中△ABC的周长(结果保留根号)；

(4)画出((2)中△ABC关于y轴对称的△A'B'C'.

Answer 1

【答案】（1）详见解析；（2）(-1，1)；（3）2+2；（4）详见解析.

【解析】

（1）把点A向右平移2个单位，向下平移4个单位就是原点的位置，建立相应的平面直角坐标系；
（2）作线段AB的垂直平分线，寻找满足腰长是无理数的点C即可；
（3）利用格点三角形分别求出三边的长度，即可求出△ABC的周长；
（4）分别找出A、B、C关于y轴的对称点，顺次连接即可．

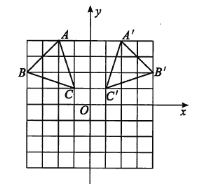
解：(1)建立平面直角坐标系如图所示；

(2)(-1，1)；

(3)AB==2,

BC=AC==,

∴△ABC的周长=2+2；

(4)画出△A'B'C′如图所示.