题目内容
【题目】如图,在平面直角坐标系中,直线AB与x轴交于点A(﹣2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线y=![]() (k≠0)上,则k的值为( )
(k≠0)上,则k的值为( )
A.4
B.-2
C.![]()
D.-![]()
【答案】D
【解析】如图,设点C的坐标为(x,y),过点C作CD⊥x轴,作CE⊥y轴,∵将△ABO沿直线AB翻折,
∴∠CAB=∠OAB=30°,AC=AO=2,∠ACB=AOB=90°,∴CD=y=ACsin60°=2×![]() =
=![]() ,∵∠ACB=∠DCE=90°,∴∠BCE=∠ACD=30°,
,∵∠ACB=∠DCE=90°,∴∠BCE=∠ACD=30°,
∵BC=BO=AOtan30°=2×![]() =
=![]() ,CE=x=BCcos30°=
,CE=x=BCcos30°=![]() =1,∵点C恰好落在双曲线y=
=1,∵点C恰好落在双曲线y=![]() (k≠0)上,∴k=xy=﹣1×
(k≠0)上,∴k=xy=﹣1×![]() =﹣
=﹣![]() ,
,
故选D.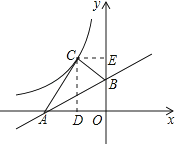
【考点精析】解答此题的关键在于理解翻折变换(折叠问题)的相关知识,掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
【题目】某种商品的进价为40元/件,以获利不低于25%的价格销售时,商品的销售单价y(元/件)与销售数量x(件)(x是正整数)之间的关系如下表:
x(件) | … | 5 | 10 | 15 | 20 | … |
y(元/件) | … | 75 | 70 | 65 | 60 | … |
(1)由题意知商品的最低销售单价是___元,当销售单价不低于最低销售单价时,y是x的一次函数.求出y与x的函数关系式及x的取值范围;
(2)在(1)的条件下,当销售单价为多少元时,所获销售利润最大,最大利润是多少元?