Question

【题目】如图，菱形ABCD的对角线AC，BD相交于点O，分别延长OA，OC到点E，F，使AE=CF，依次连接B，F，D，E各点．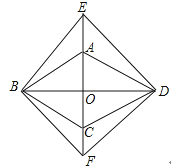

（1）求证：△BAE≌△BCF
（2）若∠ABC=50°，则当∠EBA=°时，四边形BFDE是正方形．

Answer 1

【答案】
（1）

证明：∵ 菱形ABCD的对角线AC，BD相交于点O，∴ AB=BC，∠BAC=∠BCA，∴ ∠BAE=∠BCF，

在△BAE与△BCF中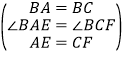， ∴ △BAE≌△BCF（SAS）

（2）20
【解析】（2）∵四边形BFDE对角线互相垂直平分，∴只要∠EBF=90°即得四边形BFDE是正方形，∵△BAE≌△BCF，∴∠EBA=∠FBC，又∵∠ABC=50°，
∴∠EBA+∠FBC=40°，∴∠EBA=×40°=20°．故答案为：20
（1）由题意易证∠BAE=∠BCF，又因为BA=BC，AE=CF，于是可证△BAE≌△BCF；（2）由已知可得四边形BFDE对角线互相垂直平分，只要∠EBF=90°即得四边形BFDE是正方形，由△BAE≌△BCF可知∠EBA=∠FBC，又由∠ABC=50°，可得∠EBA+∠FBC=40°，于是∠EBA=×40°=20°．