题目内容
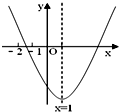
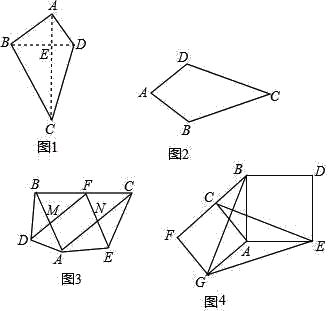
【题目】阅读理解:如图1,我们把对角线互相垂直的四边形叫做垂美四边形.垂美四边形有如下性质:
垂美四边形的两组对边的平方和相等.
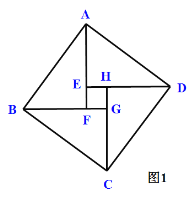
已知:如图1,四边形ABCD是垂美四边形,对角线AC、BD相交于点E.
求证:AD2+BC2=AB2+CD2
证明:∵四边形ABCD是垂美四边形
∴AC⊥BD,
∴∠AED=∠AEB=∠BEC=∠CED=90°,
由勾股定理得,AD2+BC2=AE2+DE2+BE2+CE2,
AB2+CD2=AE2+BE2+CE2+DE2,
∴AD2+BC2=AB2+CD2.
拓展探究:
(1)如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由.
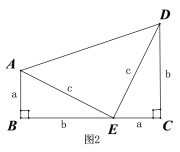
(2)如图3,在Rt△ABC中,点F为斜边BC的中点,分别以AB,AC为底边,在Rt△ABC外部作等腰三角形ABD和等腰三角形ACE,连接FD,FE,分别交AB,AC于点M,N.试猜想四边形FMAN的形状,并说明理由;
问题解决:
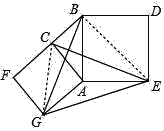
如图4,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5.求GE长.
【答案】拓展探究:(1)四边形ABCD是垂美四边形,理由详见解析;(2)四边形FMAN是矩形,理由详见解析;问题解决:![]() .
.
【解析】
(1)根据垂直平分线的判定定理可得直线AC是线段BD的垂直平分线,进而得证;
(2)首先猜想出结论,根据垂直的定义可得∠AOD=∠AOB=∠BOC=∠COD=90°,由勾股定理得AD2+BC2=AO2+DO2+BO2+CO2,进而证得猜想,将已知代入即可求得CD;
(3)根据垂美四边形的性质、勾股定理、结合(2)的结论计算即可.
拓展探究:(1)四边形ABCD是垂美四边形,
理由如下:
∵AB=AD,
∴点A在线段BD的垂直平分线上,
∵CB=CD,
∴点C在线段BD的垂直平分线上,
∴直线AC是线段BD的垂直平分线,
∴AC⊥BD,即四边形ABCD是垂美四边形.
(2)四边形FMAN是矩形,
理由:如图3,连接AF,
∵Rt△ABC中,点F为斜边BC的中点,
∴AF=CF=BF,
又∵等腰三角形ABD和等腰三角形ACE,
∴AD=DB、AE=CE,
∴由(1)可得,DF⊥AB,EF⊥AC,
又∵∠BAC=90°,
∴∠AMF=∠MAN=∠ANF=90°,
∴四边形AMFN是矩形;
问题解决:
连接CG、BE,
∵∠CAG=∠BAE=90°,
∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,
∵在△GAB和△CAE中,AG=AC,∠GAB=∠CAE,AB=AE,
∴△GAB≌△CAE,
∴∠ABG=∠AEC,
又∠AEC+∠AME=90°,
∴∠ABG+∠AME=90°,即CE⊥BG,
∴四边形CGEB是垂美四边形,
∴CG2+BE2=CB2+GE2,
∵AC=4,AB=5,
∴BC=3,CG=![]() ,BE=
,BE=![]() ,
,
∴GE2=CG2+BE2﹣CB2=73,
∴GE=![]()

 名校课堂系列答案
名校课堂系列答案