题目内容
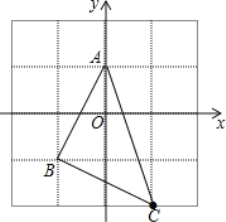
【题目】如图:在4×4的网格中存在线段AB,每格表示一个单位长度,并构建了平面直角坐标系.
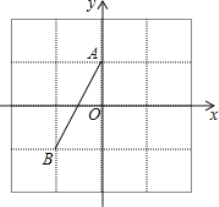
(1)直接写出点A、B的坐标:A( , ),B( , );
(2)请在图中确定点C(1,﹣2)的位置并连接AC、BC,则△ABC是 三角形(判断其形状);
(3)在现在的网格中(包括网格的边界)存在一点P,点P的横纵坐标为整数(在格点上),连接PA、PB后得到△PAB为等腰三角形,则满足条件的点P有 个.
【答案】(1)0,1,-1,-1;(2)等腰直角;(3)8.
【解析】
(1)根据平面直角坐标系可直接写出A、B的坐标;
(2)画出图形,利用勾股定理计算出AB2、CB2、AC2,再利用逆定理证明△ACB是等腰直角三角形;
(3)分别以A、B为圆心,AB长为半径画圆可得P的位置及个数.
(1)根据平面直角坐标系可得A(0,1),B(-1,-1),
故答案为:0;1;-1;-1;
(2)∵AB2=12+22=5,CB2=12+22=5,AC2=12+32=10,
∴AB2+BC2=AC2,
∴△ACB是等腰直角三角形,
故答案为:等腰直角;
(3)如图所示: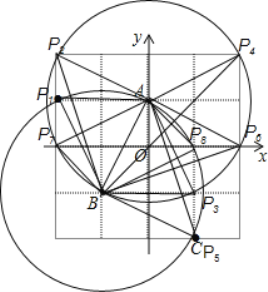 ,
,
满足条件的点P有8个,
故答案为:8.

【题目】为了解某市初三学生的体育测试成绩和课外体育锻炼时间的情况,现从全市初三学生体育测试成绩中随机抽取200名学生的体育测试成绩作为样本.体育成绩分为四个等次:优秀、良好、及格、不及格.
体育锻炼时间 | 人数 |
4≤x≤6 |
|
2≤x<4 | 43 |
0≤x<2 | 15 |
(1)试求样本扇形图中体育成绩“良好”所对扇形圆心角的度数;
(2)统计样本中体育成绩“优秀”和“良好”学生课外体育锻炼时间表(如图表所示),请将图表填写完整(记学生课外体育锻炼时间为x小时);
(3)全市初三学生中有14400人的体育测试成绩为“优秀”和“良好”,请估计这些学生中课外体育锻炼时间不少于4小时的学生人数.