��Ŀ����
����Ŀ���Ķ�̽��
���ⱳ����������ѧ�һ�������������ι�ϵ�������ɶ�������������������Ϊ�������������������������е�һ����̸����������.2002��8���ڱ����ٿ��Ĺ�����ѧ�����ȡ�����ҹ��Ŵ���ѧ����ˬ�ġ�����Բ��ͼע�����������ĸ�ȫ�ȵ�ֱ�����������м��С������ƴ�ɵ�һ���������Σ���ͼ1��ʾ��.���ɶ�����һ�����ϵ���ѧ���������кܶ���֤���������ҹ�������ѧ����ˬ������ͼ���������������֤��.
��ˬ֤���������£�
��a��bΪֱ�DZߣ�b>a������cΪб�����ĸ�ȫ�ȵ�ֱ�������Σ���ÿ��ֱ�������ε��������![]() �������ĸ�ֱ��������ƴ����ͼ1��ʾ��״.
�������ĸ�ֱ��������ƴ����ͼ1��ʾ��״.
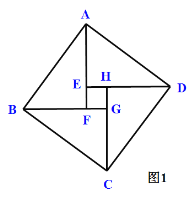
��Rt��DAE��Rt��ABF
���EDA=��FAB
�ߡ�EAD+��EDA=90��
���FAB+��EAD=90��
���ı���ABCD��һ���߳�Ϊc�������Σ������������![]()
��EF=FG=GH=HE=b-a
��HEF=90��
���ı���EFGH��һ���߳�Ϊb-a�������Σ������������![]()
��![]()
��![]() �Ӷ�֤���˹��ɶ���.
�Ӷ�֤���˹��ɶ���.
˼ά��չ��
1������������ε����Ϊ13��С�����ε����Ϊ1��ֱ�������εĽ϶�ֱ�DZ߳�Ϊa���ϳ�ֱ�DZ߳�Ϊb����ô![]() ��ֵΪ .
��ֵΪ .
2�������ڶ�ʮ����ͳ�ӷƶ���Ҳ���������˹��ɶ�����һ��֤����������ͼ2��ʾ��
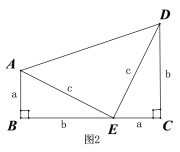
��������ȫ�ȵ�ֱ�������κ�һ������ֱ��������ƴ����һ��ֱ�����Σ��������ô�ͼ����֤���ɶ���.
֤������ֱ������ABCD��������������ַ�����ʾ��
��һ�ַ�����ʾΪ��
�ڶ��ַ�����ʾΪ��
�� =
��![]()
̽�����£�
��ֽ�����ĸ�ȫ�ȵ�ֱ�������Σ���ֱ�DZߵij��ֱ�Ϊa��b��б�߳�Ϊc�����㿪���Խ������ƴ��һ����֤�����ɶ�����ͼ�Σ���ͬ������ͼ1��ͼ2��.�뻭����ƴ�ɵ�ͼ�Σ������㻭��ͼ��֤�����ɶ���.

���𰸡�˼ά��չ��1��25��2��![]() ab+
ab+![]() ab+
ab+![]() c2��
c2��![]() ��a+b����a+b����
��a+b����a+b����![]() ab+
ab+![]() ab+
ab+![]() c2��
c2��![]() ��a+b����a+b����̽�����£������.
��a+b����a+b����̽�����£������.
��������
˼ά��չ��1���������⣬���ͼ�����ab��a2+b2��ֵ��ԭʽ������ȫƽ����ʽ����������㼴�����ֵ��
2���������ε�����͡����ε��������ʾ���ͼ�ε�������Ӷ�֤�����ɶ�����
̽�����£����ĸ�ȫ�ȵ�ֱ�������ε�б����β��ӣ���ƴ������ͼ�����ֱ������ַ�������������ε�������Ӷ��ɵý��.
˼ά��չ��1���⣺��������ã�c2=a2+b2=13��4��![]() ab=13-1=12����2ab=12��
ab=13-1=12����2ab=12��
��a+b��2=a2+2ab+b2=13+12=25��
�ʴ�Ϊ��25��
2���⣺��ͼ���Կ���������ֱ�������ε�����ͣ�����ֱ�Ϊ![]() ab��
ab��![]() ab��
ab��![]() c2��
c2��
���ͼ�����Ϊ![]() ab+
ab+![]() ab+
ab+![]() c2��
c2��
�����Կ���һ��ֱ�����Σ������Ϊ![]() ��a+b����a+b����
��a+b����a+b����
��![]() ab+
ab+![]() ab+
ab+![]() c2=
c2=![]() ��a+b����a+b��.
��a+b����a+b��.
̽�����£��⣺��ͼ��ʾ��
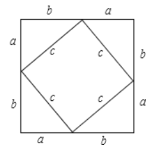
֤�����ߴ������ε�����ɱ�ʾΪ��a+b��2��
�������ε����Ҳ�ɱ�ʾΪ��c2+4��![]() ab��
ab��
�ࣨa+b��2=c2+4��![]() ab��
ab��
��a2+b2+2ab=c2+2ab��
��a2+b2=c2��
��ֱ����������ֱ�DZߵ�ƽ���͵���б�ߵ�ƽ����