题目内容
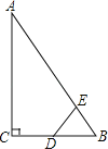
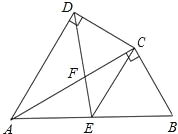
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=ABAD;
(2)求证:△AFD∽△CFE.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据两组对角对应相等的两个三角形相似证明即可;
(2)根据直角三角形的性质得到CE=BE=AE,根据等腰三角形的性质得到∠EAC=∠ECA,推出AD∥CE即可解决问题;
(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴AD:AC=AC:AB,
∴AC2=ABAD;
(2)证明:∵E为AB的中点,
∴CE=BE=AE,
∴∠EAC=∠ECA,
∵∠DAC=∠CAB,
∴∠DAC=∠ECA,
∴CE∥AD,
∴△AFD∽△CFE.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目