Question

【题目】在Rt△ABC中，AB＝6，BC＝8，则这个三角形的内切圆的半径是( )

A.5B.2C.5或2D.2或－1

Answer 1

【答案】D

【解析】

分AC为斜边和BC为斜边两种情况讨论.根据切线定理得过切点的半径垂直于三角形各边，利用面积法列式求半径长.

第一情况：当AC为斜边时，

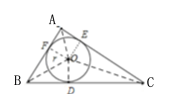
如图，设⊙O是Rt△ABC的内切圆，切点分别为D,E,F,连接OC,OA,OB,

∴OD⊥AC, OE⊥BC,OF⊥AB,且OD=OE=OF=r,

在Rt△ABC中，AB＝6，BC＝8，由勾股定理得，

,

∵ ,

∴ ,

∴ ,

∴r=2.

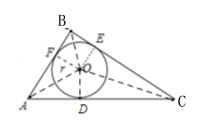
第二情况：当BC为斜边时，

如图，设⊙O是Rt△ABC的内切圆，切点分别为D,E,F,连接OC,OA,OB,

∴OD⊥BC, OE⊥AC,OF⊥AB,且OD=OE=OF=r,

在Rt△ABC中，AB＝6，BC＝8，由勾股定理得，

,

∵ ,

∴ ,

∴ ,

∴r= .

故选：D.