Question

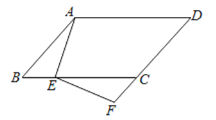
【题目】如图，在ABCD中，AB＝4，BC＝8，∠ABC＝60°．点P是边BC上一动点，作△PAB的外接圆⊙O交BD于E．

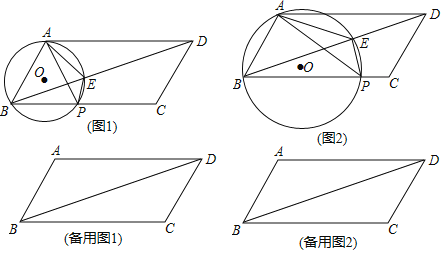
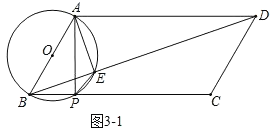
（1）如图1，当PB＝3时，求PA的长以及⊙O的半径；

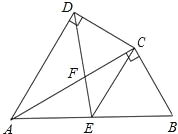
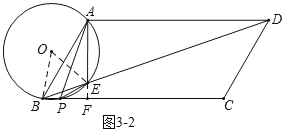
（2）如图2，当∠APB＝2∠PBE时，求证：AE平分∠PAD；

（3）当AE与△ABD的某一条边垂直时，求所有满足条件的⊙O的半径．

Answer 1

【答案】（1）PA的长为，⊙O的半径为；（2）见解析；（3）⊙O的半径为2或或

【解析】

（1）过点A作BP的垂线，作直径AM，先在Rt△ABH中求出BH，AH的长，再在Rt△AHP中用勾股定理求出AP的长，在Rt△AMP中通过锐角三角函数求出直径AM的长，即求出半径的值；

（2）证∠APB＝∠PAD＝2∠PAE，即可推出结论；

（3）分三种情况：当AE⊥BD时，AB是⊙O的直径，可直接求出半径；当AE⊥AD时，连接OB，OE，延长AE交BC于F，通过证△BFE∽△DAE，求出BE的长，再证△OBE是等边三角形，即得到半径的值；当AE⊥AB时，过点D作BC的垂线，通过证△BPE∽△BND，求出PE，AE的长，再利用勾股定理求出直径BE的长，即可得到半径的值．

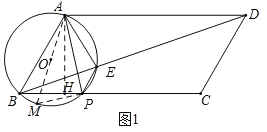
（1）如图1，过点A作BP的垂线，垂足为H，作直径AM，连接MP，

在Rt△ABH中，∠ABH＝60°，

∴∠BAH＝30°，

∴BH＝AB＝2，AH＝ABsin60°＝2，

∴HP＝BP﹣BH＝1，

∴在Rt△AHP中，

AP＝＝，

∵AB是直径，

∴∠APM＝90°，

在Rt△AMP中，∠M＝∠ABP＝60°，

∴AM＝＝＝，

∴⊙O的半径为，

即PA的长为，⊙O的半径为；

（2）当∠APB＝2∠PBE时，

∵∠PBE＝∠PAE，

∴∠APB＝2∠PAE，

在平行四边形ABCD中，AD∥BC，

∴∠APB＝∠PAD，

∴∠PAD＝2∠PAE，

∴∠PAE＝∠DAE，

∴AE平分∠PAD；

（3）①如图3﹣1，当AE⊥BD时，∠AEB＝90°，

∴AB是⊙O的直径，

∴r＝AB＝2；

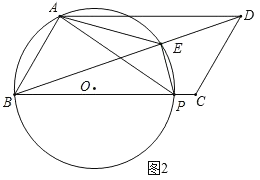
②如图3﹣2，当AE⊥AD时，连接OB，OE，延长AE交BC于F，

∵AD∥BC，

∴AF⊥BC，△BFE∽△DAE，

∴＝，

在Rt△ABF中，∠ABF＝60°，

∴AF＝ABsin60°＝2，BF＝AB＝2，

∴＝，

∴EF＝，

在Rt△BFE中，

BE＝＝＝，

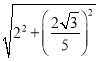∵∠BOE＝2∠BAE＝60°，OB＝OE，

∴△OBE是等边三角形，

∴r＝；

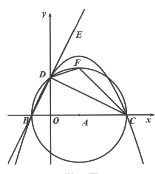
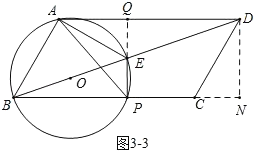
③当AE⊥AB时，∠BAE＝90°，

∴AE为⊙O的直径，

∴∠BPE＝90°，

如图3﹣3，过点D作BC的垂线，交BC的延长线于点N，延开PE交AD于点Q，

在Rt△DCN中，∠DCN＝60°，DC＝4，

∴DN＝DCsin60°＝2，CN＝CD＝2，

∴PQ＝DN＝2，

设QE＝x，则PE＝2﹣x，

在Rt△AEQ中，∠QAE＝∠BAD﹣BAE＝30°，

∴AE＝2QE＝2x，

∵PE∥DN，

∴△BPE∽△BND，

∴＝，

∴＝，

∴BP＝10﹣x，

在Rt△ABE与Rt△BPE中，

AB2+AE2＝BP2+PE2，

∴16+4x2＝（10﹣x）2+（2﹣x）2，

解得，x1＝6（舍），x2＝，

∴AE＝2，

∴BE＝＝＝2，

∴r＝，

∴⊙O的半径为2或或．