题目内容
【题目】(重温旧知)圆内接四边形的内角具有特殊的性质.
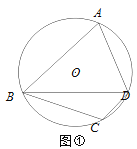
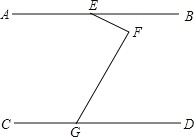
如图①,四边形ABCD是⊙O的内接四边形,若AB=BD,∠ABD=50°,则∠BCD=_______°.
(提出问题)圆内接四边形的边会有特殊性质吗?
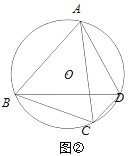
如图②,某数学兴趣小组进行深入研究发现:ABCD+BCDA=ACBD,请按他们的思路继续完成证明.
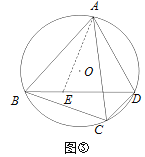
证明:如图③,作∠BAE=∠CAD,交BD于点E.
∵∠BAE=∠CAD,∠ABD=∠ACD,
∴△ABE∽△ACD,
∴![]() 即ABCD=ACBE
即ABCD=ACBE
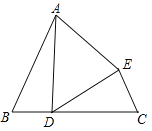
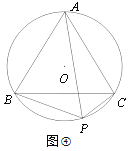
(应用迁移)如图,已知等边△ABC外接圆⊙O,点P为![]() 上一点,且PB=
上一点,且PB=![]() ,PC=1,求PA的长.
,PC=1,求PA的长.
【答案】115
【解析】分析:(1)、根据圆内角四边形的对角互补以及等腰三角形的性质得出答案;(2)、根据题意得出△ABC和△AED相似,从而得出ADBC=ACDE,从而根据ABCD+ADBC=ACBE+ACDE得出答案;(3)、根据(2)得出PBAC+PCAB=PABC,根据等边三角形的性质得出(PB+PC)BC= PABC,从而得出答案.
详解:(1)115
(2)证明:如图3,
∵∠BAE=∠CAD ∴∠BAE+∠CAE=∠CAD+∠CAE,即∠BAC=∠DAE,
又∵∠ACB=∠ADB,∴△ABC∽△AED,∴![]() ,即ADBC=ACDE ,
,即ADBC=ACDE ,
∴ABCD+ADBC=ACBE+ACDE, ∴ABCD+BCDA=ACBD,
(3)由(2)可知PBAC+PCAB=PABC
∵△ABC是等边三角形, ∴AB=AC=BC,∴(PB+PC)BC= PABC,
∴PB+PC= PA即PA=![]() +1.
+1.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目