Question

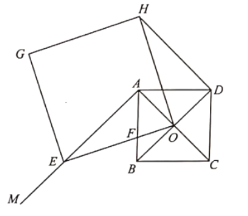
【题目】如图，已知正方形中，相交于点，过点作射线，点是射线上一动点，连接交于点，以为一边，作正方形，且点在正方形的内部，连接．

（1）求证：；

（2）设，正方形的边长为，求关于的函数关系式，并写出定义域；

（3）连接，当是等腰三角形时，求的长．

Answer 1

【答案】（1）详见解析；（2）（）；（3）当是等腰三角形时，或

【解析】

（1）根据正方形的性质得到∠AOD=90°，AO=OD，∠EOH=90°，OE=OH，由全等三角形的性质即可得到结论；

（2）如图1，过O作ON⊥AB于N，根据等腰直角三角形的性质得到，

根据勾股定理得到，根据平行线分线段成比例定理即可得到结论；

（3）①当AE=EG时，△AEG是等腰三角形，②当AE=AG时，△AEG是等腰三角形，如图2，过A作AP⊥EG于P③当GE=AG时，△AEG是等腰三角形，如图3，过G作GQ⊥AE于Q，根据相似三角形的性质或全等三角形的性质健即可得到结论．

（1）∵四边形是正方形，

，

，

∵四边形是正方形，

，

，

，

即，

．

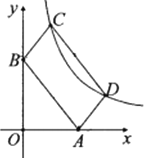
（2）如图1，过O作ON⊥AB于N，

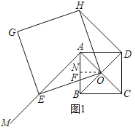
则，

∵BF=x，

∴AF=4-x，

∴FN=2-x，

∴，

∴，

∵AM⊥AC，

∴AE∥OB，

∴，

∴，

∴；

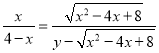（3）①当AE=EG时，△AEG是等腰三角形，则AE=OE，

∵∠EAO=90°，

∴这种情况不存在；

②当AE=AG时，△AEG是等腰三角形，

如图2，过A作AP⊥EG于P，则AP∥OE，

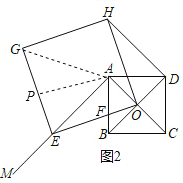
∴∠PAE=∠AEO，

∴△APE∽△EAO，

∴，

∵AE=AG，

∴，，

∴，

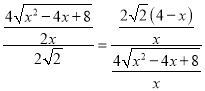解得：x=2，

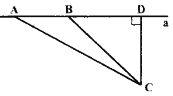
②当GE=AG时，△AEG是等腰三角形，

如图3，过G作GQ⊥AE于Q，

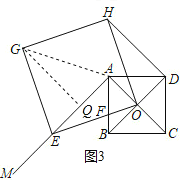
∴∠GQE=∠EAO=90°，

∴∠GEQ+∠EGQ=∠GEQ+∠AEO=90°，

∴∠EGQ=∠AEO，

∵GE=OE，

∴△EGQ≌△OEA（AAS），

∴，

∴，

∴，

∴BF=2或．